2024-05-06-CSAPP2_信息表示与处理

2024-05-06

用比特表示信息

一切均是比特位

每个比特是0或1 以各种方式编码/解释比特位串

使用比特位的好处

易于用稳态元件存储(联系数电) 在有噪声和不精确的电缆中可靠传输

二进制数

性质

\(1+\sum_{i=0}^{w-1}2^i=2^w\) 证明：

  • $w=0$，有$1=2^0$
  • 假设对于$w-1$为真
    • $1 + 1+2+4+8+\cdots + 2^{w-1}+2^w=2^w+2^w = 2^{w+ 1}$

多个位组成group

通过多个bit组成的组来表示某个数 image.png

进制转换

十进制-十六进制-二进制之间的互相转换(此处仅举例，需要多练习) image.png

组合字节bytes以创建标量数据类型

image.png

比特级操作

  • 布尔运算：与、或、非、异或
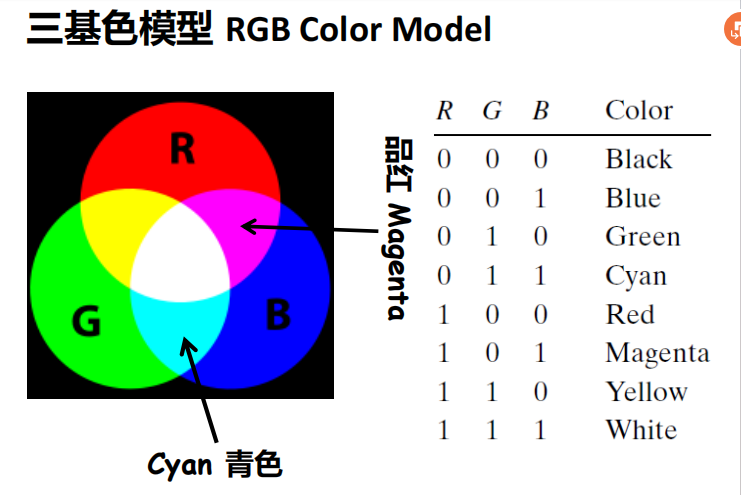
  • 小整数集合，是否在集合中用01表示 image.png
  • 三基色模型 image.png

比特位异或

  • 比特位级异或是一种加法
  • 具有额外的性质，即每个值都是其自身的加法逆元 A ^ A = 0 A ^ 0 = A

通过异或进行交换

int inplace_swap(int *x, int *y){
	*x = *x ^ *y;  // x ^ y
	*y = *x ^ *y;  // x
	*x = *x ^ *y;  // y
}

// 尝试对数组进行逆序
void reverse_array(int a[], int cnt){
	int first, last;
	for(first = 0, last = cnt - 1; first <= last; first ++, last--)
		inplace_swap(&a[first], &a[last]);
}

使用异或操作符(^)进行变量交换是一种非常巧妙的方法，因为它不需要额外的临时变量。这段代码中的inplace_swap函数通过三次异或操作来交换两个整数指针指向的值。然而，这种方法存在一个潜在的问题，尤其是在first == last的情况下。

当first == last时，即数组索引指向同一个元素，按照inplace_swap函数的逻辑：

  1. *x = *x ^ *y; 此时*x和*y指向同一个地址，所以这个操作相当于x = x ^ x，结果为0。
  2. *y = *x ^ *y; 由于第一步已经将*x置为0，所以这里*y变为0。
  3. *x = *x ^ *y; 这里*x和*y都是0，所以*x再次变为0。 最终结果是，原本的值被错误地置为0，而不是保持不变。这显然是不正确的，因为当索引相同时，我们并不希望改变该元素的值。

正确的处理方式是，在进行异或交换之前，先检查first和last是否相等。如果相等，则不需要进行任何操作，因为这意味着元素不需要交换，它已经是数组中的最后一个元素，同时也是第一个元素。 但是最好还是不用异或进行交换(笑)

掩码操作

掩码操作在编程和计算机科学中是一种常用的技术，它涉及到使用位运算来操作数据。掩码通常是一个二进制数，用来选择、修改或保护数据中的特定部分。

  1. 效率：位运算（如AND、OR、XOR、NOT）在硬件层面上执行得非常快，因为它们可以直接在处理器的算术逻辑单元（ALU）中进行，不需要额外的内存访问。
  2. 精确控制：掩码操作允许程序员精确地控制哪些位被操作，这在硬件编程、嵌入式系统、网络编程等领域尤为重要。
  3. 数据打包：在某些情况下，多个小的数据项可能会被打包到一个较大的数据结构中。掩码操作可以用来访问或修改这些数据项中的特定部分。
  4. 状态标志：在某些算法中，掩码可以用来表示多个状态或标志。通过位运算，可以快速地设置、清除或检查这些状态。
  5. 优化存储：通过使用掩码，可以在不使用额外存储空间的情况下，将多个布尔值或小的数据项编码到单个整数中。
  6. 安全性：在加密和安全领域，掩码操作可以用来保护数据，防止未授权访问。
例子，常用的掩码0xFF

最低8个有效位为1，指明一个字的最低字节(一个字两个字节(32位系统))

X = 0x89ABCDEF
X & 0xFF = 0x000000EF = 0xEF
另一个常用掩码 ~0

使用~0作为掩码的原因：

  1. 全位掩码：~0提供了一个全1的位模式，这意味着它可以用来与任何位模式进行AND操作，从而选择所有位。
  2. 简化代码：使用~0可以简化代码，因为它是一个简单的单行表达式，易于理解和维护。
  3. 位操作：在进行位操作时，~0可以用来清除一个位字段中的所有位，或者与另一个值进行AND操作来选择特定的位。
  4. 性能：在某些情况下，使用~0作为掩码可以提高代码的性能，因为它避免了使用更多的指令内存访问。
  5. 通用性：~0作为掩码是通用的，因为它不依赖于特定的数据类型或大小(比0xFFFFFFFF好的原因)。在任何整数类型上使用~0都会得到一个全1的掩码。
  6. 位域操作：在位域或打包结构体中，~0可以用来操作特定的位域，通过与~0进行AND或OR操作来设置或清除位域。
  7. 位掩码生成：~0可以与其他位掩码进行AND或OR操作，以生成更复杂的位掩码。
  8. 兼容性：~0作为掩码在几乎所有编程语言和平台上都是有效的，因为它依赖于基本的位操作，这些操作在所有现代计算机架构中都是支持的。
  9. 调试：在调试过程中，~0可以用来快速地设置或清除所有位，以测试代码的不同部分。
  10. 位测试：~0可以用来测试一个位字段是否为全1或全0，这对于某些算法或条件检查非常有用。
简单的掩码操作
x = 0x87654321
// 保留最低有效字节
x & 0xFF

// 最低有效字节不变，其他位取反
x ^ ~0xFF

// x的最低有效字节设置为全1，所有其它字节保持不变
x | 0xFF
位设置和位清除 Bis & Bic

设置结果z为x并进行修改

  • z = bis (int x, int m) (位设置 bit set) = x | m 在m为1的每个位置上，将结果z的对应位设置为1
  • z = bic(int x, int m) (位清除 bit clear) = x & ~m 在m为1的每个位置上，将结果z的对应位设置为0

可以通过这两个操作实现一些布尔运算

x | y == bis(x, y)
x ^ y == (x & ~y) | (y & ~x) == bis(bic(x, y), bic(y,x))

注意位运算和逻辑运算的不同

  • 逻辑运算：&&,   , !
    • 0等价于false
    • 任何非0视为true
    • 总是返回0或1
    • 提前终止
!0x41 => 0x00
!0x00 => 0x01
!!0x41 => 0x01

0x69 && 0x55 => 0x01
0x69 || 0x55 => 0x01

短路逻辑

  • a && 5/a
    • 如果a为零，不会计算5/a，避免了被0除
  • p && *p
    • 不会导致间接引用空指针
  • 仅使用位级和逻辑操作实现x==y->!(x^y)

移位运算

  • 左移 x << y
    • 丢弃左边多于比特，右边填0
  • 右移
    • 逻辑移位
      • 左边填0
    • 算数移位
      • 左边赋值最高有效位
  • 未定义行为：移位量小于0或大于等于字长 image.png 注意C语言中移位操作符优先级低于+-*/

例子：位计数，统计字中1的个数

不使用循环，只使用位运算进行实现

int bitCount(int x) {
	int m1 = 0x11 | (0x11 << 8); // 00010001; 0001000100000000
	// m1 = 0001000100010001
	//m1是int类型，4字节。前面还有16个0，自动脑补一下
	int mask = m1 | (m1 << 16);
	// m1 << 16 = 00010001000100010000000000000000
	//mask = 00010001000100010001000100010001
	int s = x & mask;
	s += x>>1 & mask;
	s += x>>2 & mask;
	s += x>>3 & mask;
	/* Now combine high and low order sums
	   将和组合在一起
	 */
	s = s + (s >> 16); // 前16 位和后16位的权重相加，前16位的权重还在
	// 但是我们只关注s的低16位
	/* Low order 16 bits now consists of 4 sums.
	Split into two groups and sum */
	mask = 0xF | (0xF << 8); // 1111; 111100000000;
	//0000111100001111
	//前面的0自动脑补一下，mask是int，4字节。
	s = (s & mask) + ((s >> 4) & mask); // 
	return (s + (s>>8)) & 0x3F;//00111111  32位最多只有32个1，所以3F足够，这里要掩码，所以不能用2f，但是1f只有31，位数不够，所以要用3f
}

整数

编码整数

  • 对于无符号数$B2U(X)=\sum_{i=0}^{w-1}x_i \cdot 2^i$
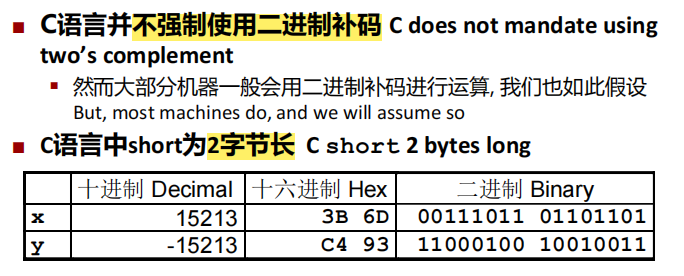
  • 对于有符号数补码 $B2T=-x_{w-1}\cdot 2^{w-1}+\sum_{i=1}^{w-2}x_i\cdot 2^i$ 补码最高有效位是符号位 image.png

补码转换

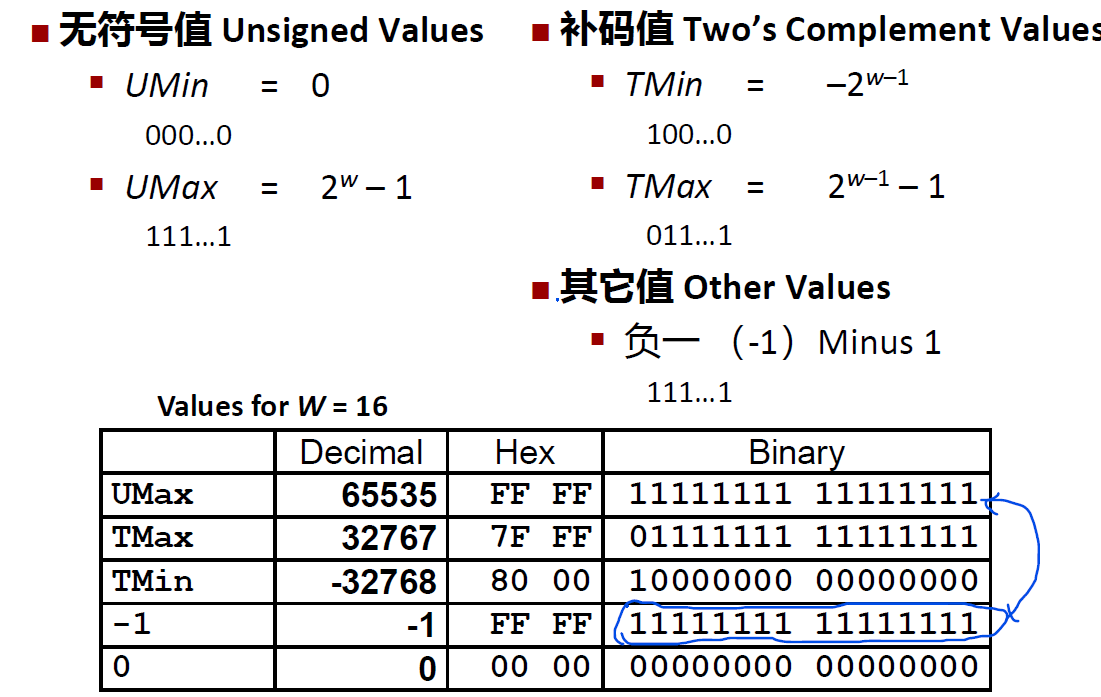  • 负数的绝对值：取反加一 image.png

数值范围

image.png 注意到$|TMin| = TMax + 1$，这个范围是不对称的（原因是有0存在） $UMax = 2 * TMax + 1$ Q: $|TMin|$是多少？ 事实上，$|TMin|$仍然为$TMin$，原因与刚刚一样，负数的绝对值是其取反加一，但这样又变回来了 例子：$TMin = 1000 0000$，但是$|TMin| = 01111111 + 1 = 10000000 = TMin$ image.png

转换与强制类型转换

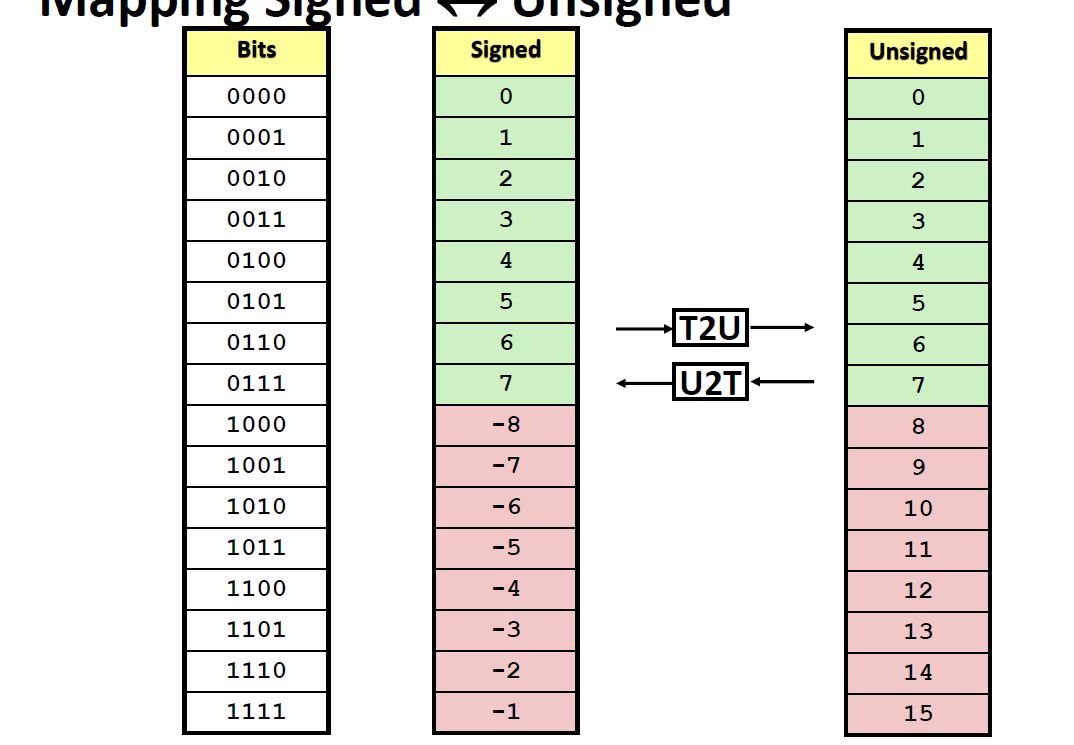
无符号数与补码之间的映射：保持位表示，数值上形成映射 \(ux=\begin{cases}x, x \ge 0\\ x+2^w, x < 0 \end{cases}\) \(tu=\begin{cases}u, u \le TMax\\ u - 2^w, u > TMax\end{cases}\) image.png|500

强制类型转换

C语言允许一种类型的变量解释为另一种数据类型

  • 常量
    • 默认为有符号整数
    • 有 u 做后缀表示无符号数
  • 强制类型转换
    • 显式强制类型转换有/无符号数等同于U2T/T2U
int tx, ty;
unsigned ux, uy;
tx= (int) ux;
uy= (unsigned)ty;
  • 隐式强制类型转换通过赋值和过程调用也会发生
tx = ux;
uy = ty;

注意

一些奇怪的比较： 如果单一表达式中混合了无符号数和有符号数，有符号值隐含强制转换成无符号数，包括比较运算 image.png

扩展和截断

零扩展

针对无符号数，如果需要转换为更大的数据类型，只需要在开头添加0

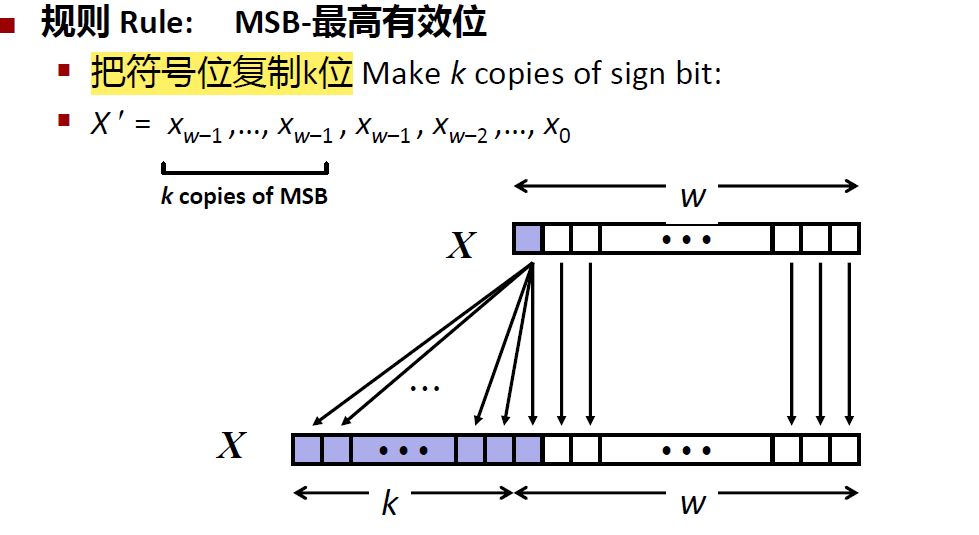
符号扩展

给定w位的带符号整数x，转换成数值相同的w+k位整数

规则

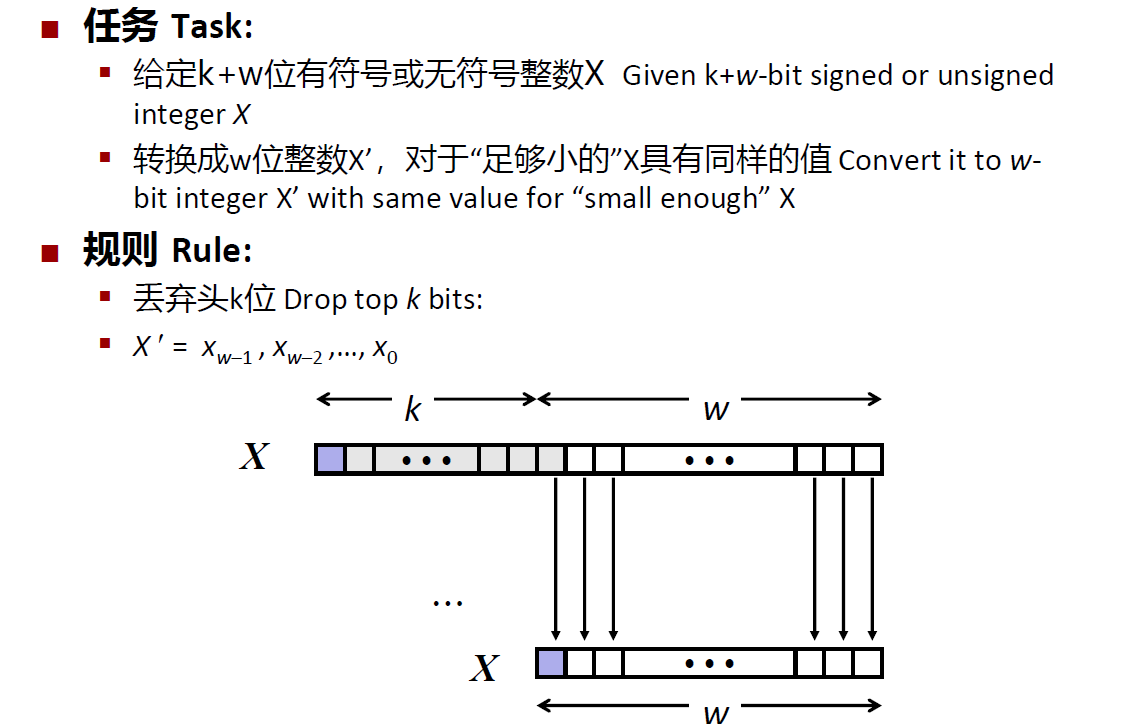
把符号位复制 k 位 image.png image.png

截断

image.png

  • 无符号数：\(x' = x\mod 2^k\)k为截断到的位数
  • 有符号数：

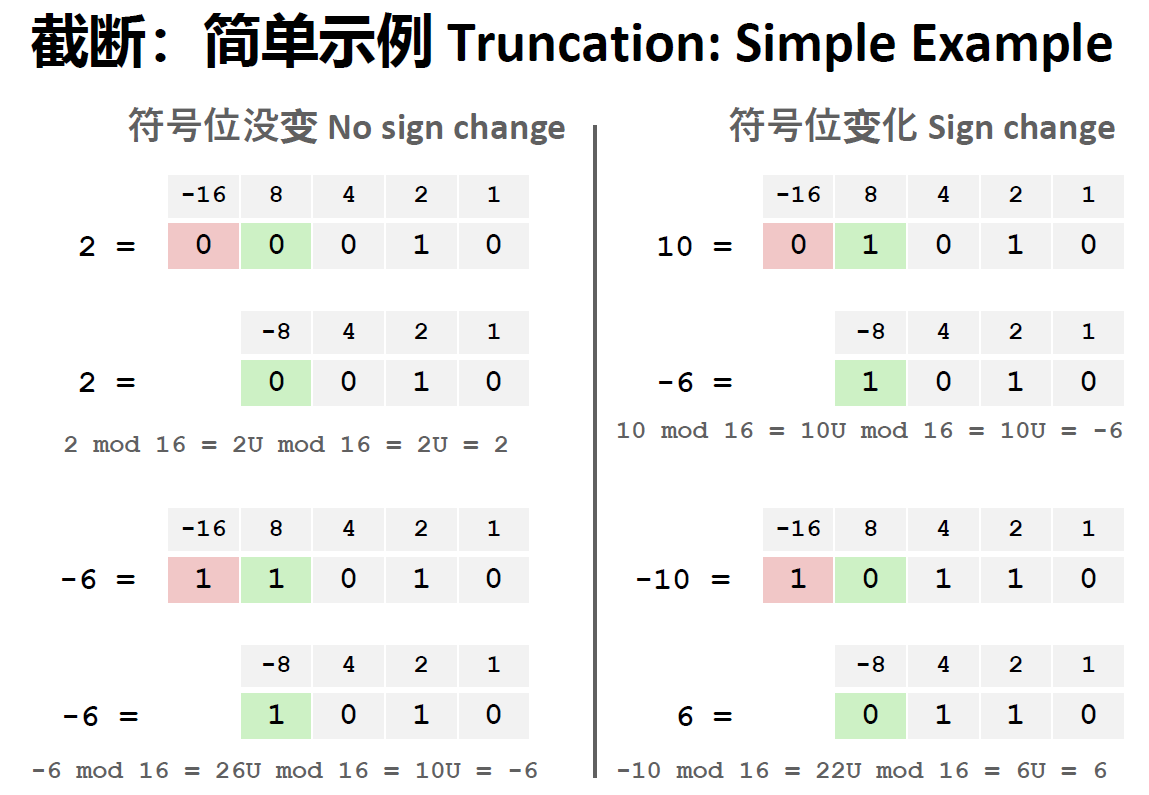image.png 先按照无符号数截断，再将无符号数转化为有符号数 \(B2T_k([x_k, x_{k-1},...,x_0])=B2T_k(B2U_W([x_w,x_{w-1},...,x_0]) \mod 2^k)\)

整数运算

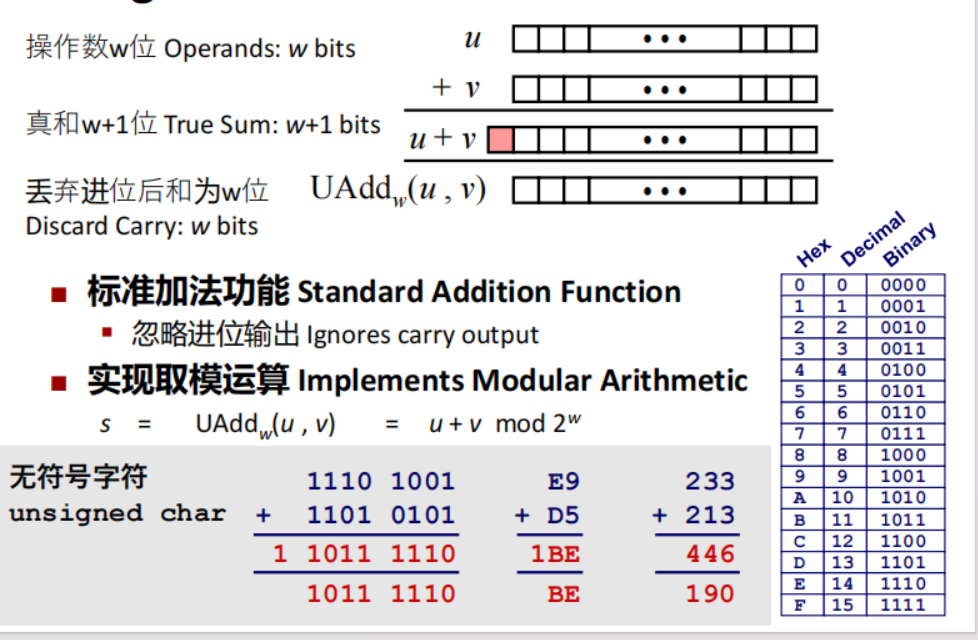
无符号数加法

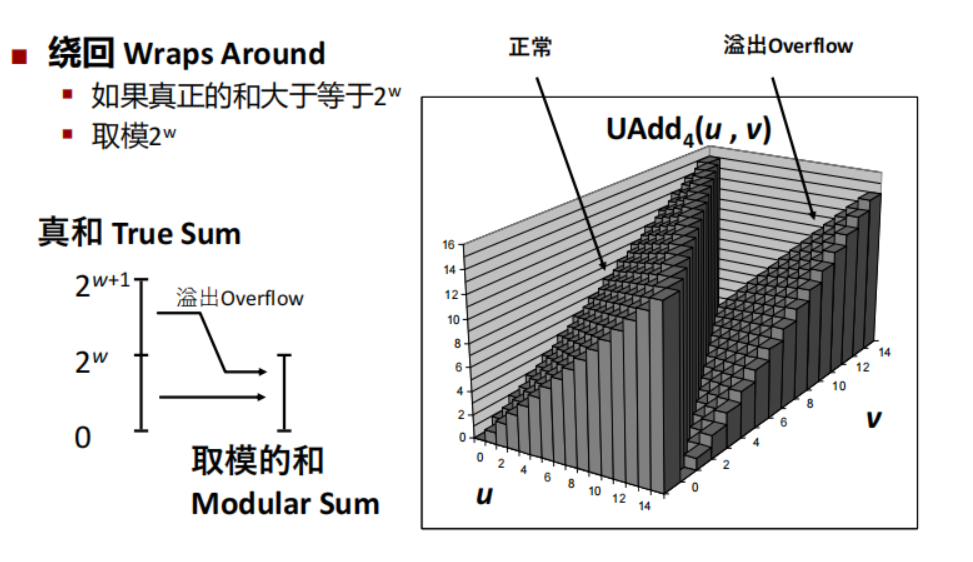
\(s = UAdd_w(u,v) = u + v \mod 2^w\) 注意区分溢出与没有溢出的情况： \(x + y^u_w=\begin{cases}x + y, &x+y < 2^w \quad 正常\\ x + y - 2 ^ w, &2^w \le x + y < 2^{w+1}\quad 溢出\end{cases}\) image.png image.png

补码加法

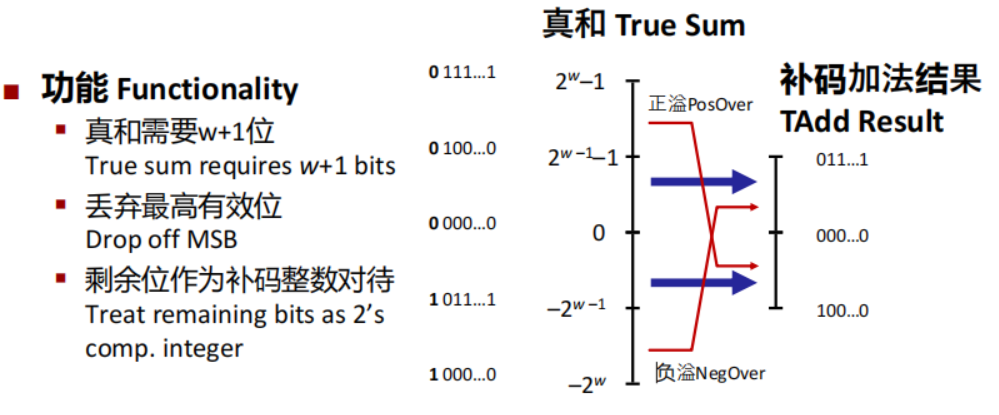
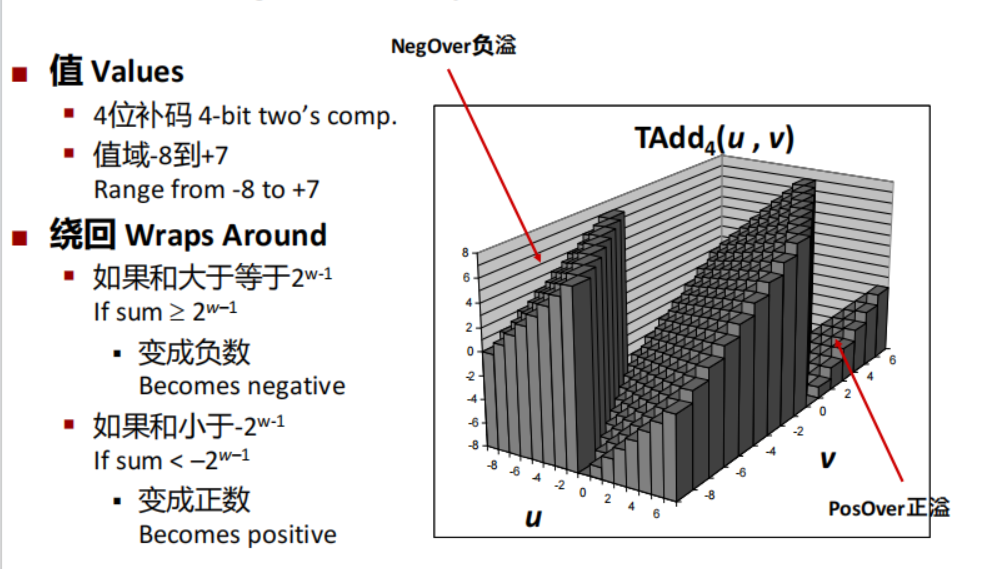
有符号和无符号数加法有同样的比特位级行为(说明只是编译器解释不同，但机器语言级别是同样的二进制位) 但是这里的溢出更为复杂，分为上(正)溢出和下(负)溢出 \(x + y^t_w=\begin{cases}x + y - 2^w, &2^{w-1} \le x + y\quad 正溢出\\x + y, &-2^{w-1}\le x+y < 2^{w-1} \quad 正常\\ x + y + 2 ^ w, & x + y < -2^{w-1}\quad 溢出\end{cases}\) image.png image.png image.png

取非

对于无符号数，其取非即为求其加法逆元，可以很容易得到： \(-x^u_w = \begin{cases}x, &x = 0\\2^w - x & x > 0\end{cases}\) 对于有符号数，注意其等于$TMin$的情况 \(-x^t_w=\begin{cases}TMin_w, &x = TMin_w\\ -x, &x > TMin_w\end{cases}\) 但是对于补码和无符号数非产生的位模式，均还是相同的，只是解释方式不同

乘法

目标：计算w位的数x和y的乘积 但是，精确的结果比w位大得多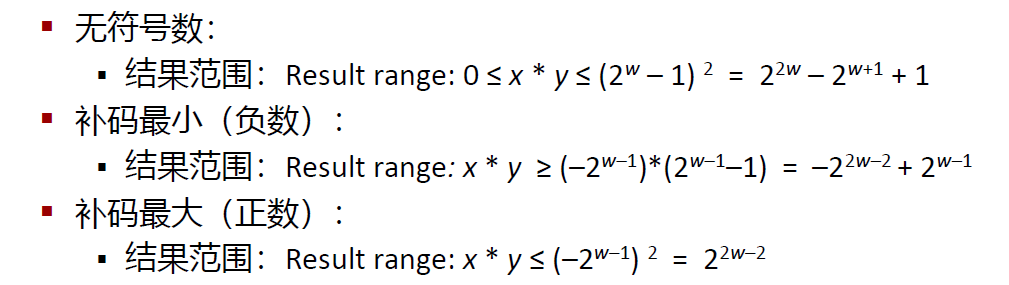： image.png 如果想要得到精确的结果，那么需要在每次计算的时候不断扩大乘积结果表示的字长 但在C语言中，通常无法保存精确结果，而是通过截断来实现保留 对于无符号数和补码乘法来说，乘法运算的位级表示都是一样的

无符号数乘法

对乘积取模即可\(x * y^u_w = (x \cdot y)\mod 2^w\) image.png

补码乘法

\(x * y^t_w = U2T_w((x \cdot y)\mod 2^w)\) image.png

[!Question] 为什么位数会不一样？ 原因之一是由于负数乘法运算，如果两个负数相乘会得到正数，因此会改变高位内容 计算乘法最好化成10进制，然后再转无符号数，再截断，最后转成补码表示

乘以常数

采用移位实现 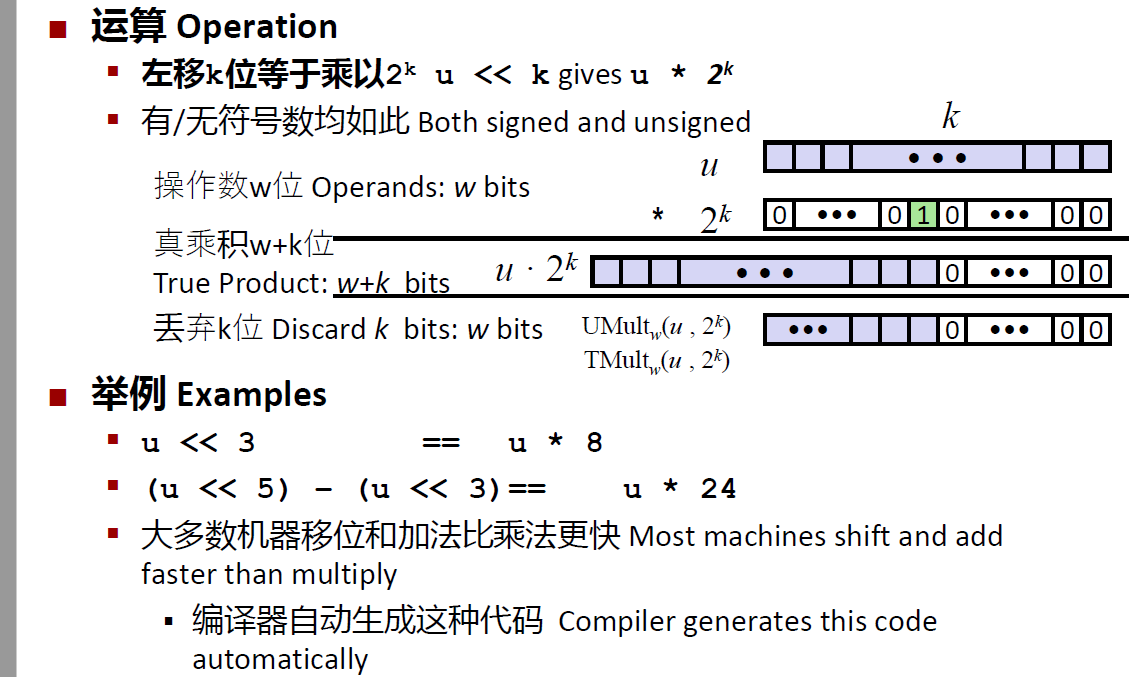image.png 注意，无论是无符号数或者补码，在乘2的幂次时都可能发生溢出，但是即使溢出，得到的值还是一样的。 eg. $1011$左移2位，得到$101100$，截取后得到$1100$

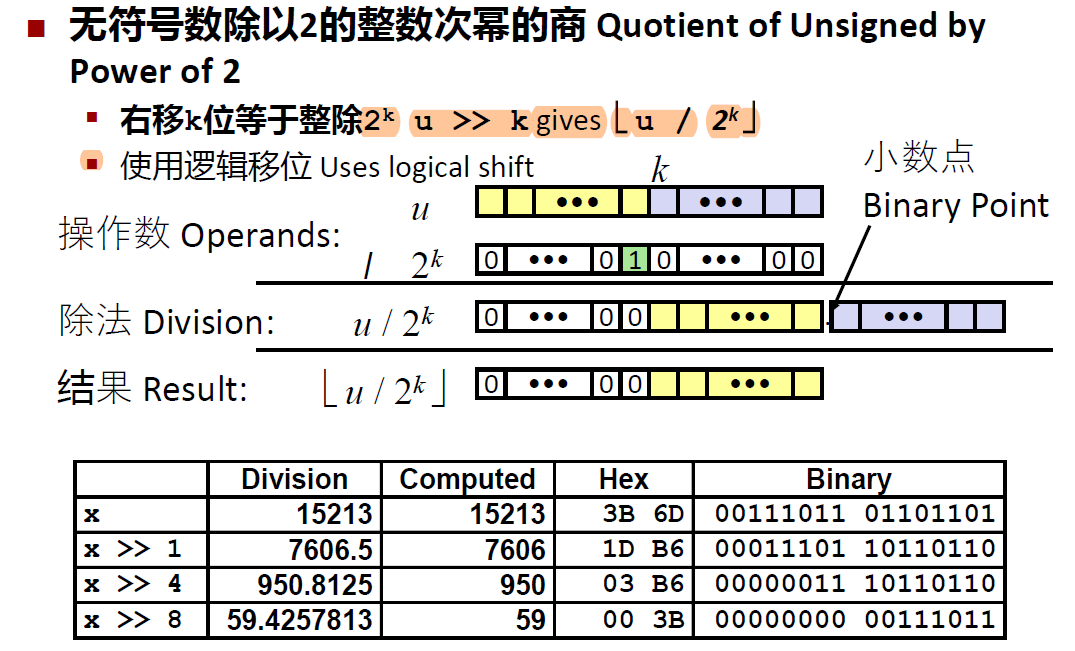
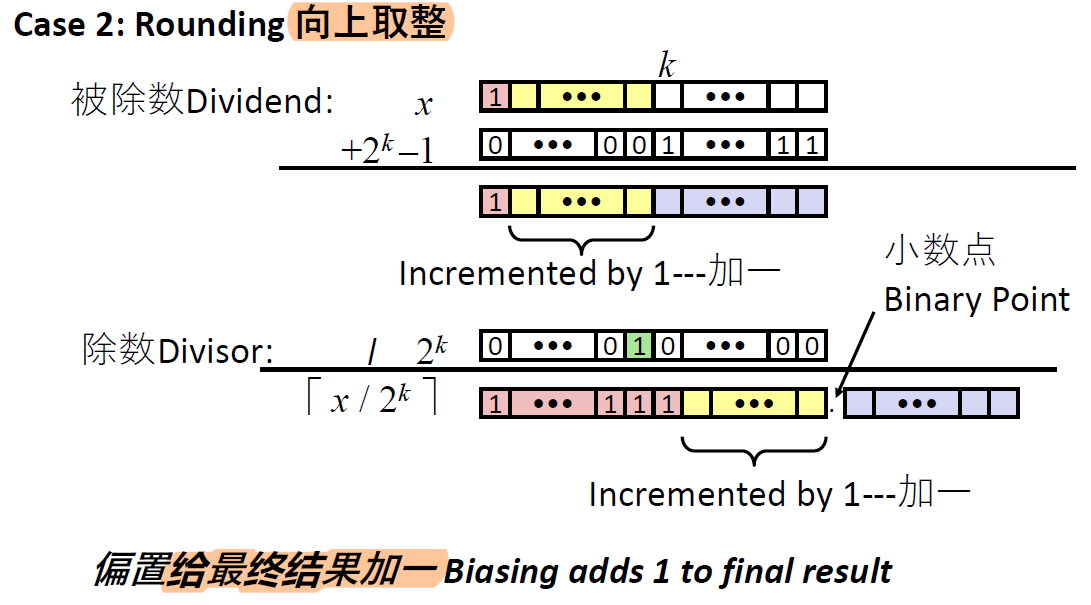
除以2的幂

无符号数：逻辑移位后向下取整 image.png

有符号数： 特殊 如果跟无符号数一样直接算数移位的话，对于非负数结果没有问题，但是对于负数，这样移位后结果会向错误的方向舍入(理论上希望向0舍入，实际变成了向下舍入) image.png 解决方式：加入“偏置(bias)”

(x + (1 << k) - 1) >> k

偏置被除数向0方向

原理证明：

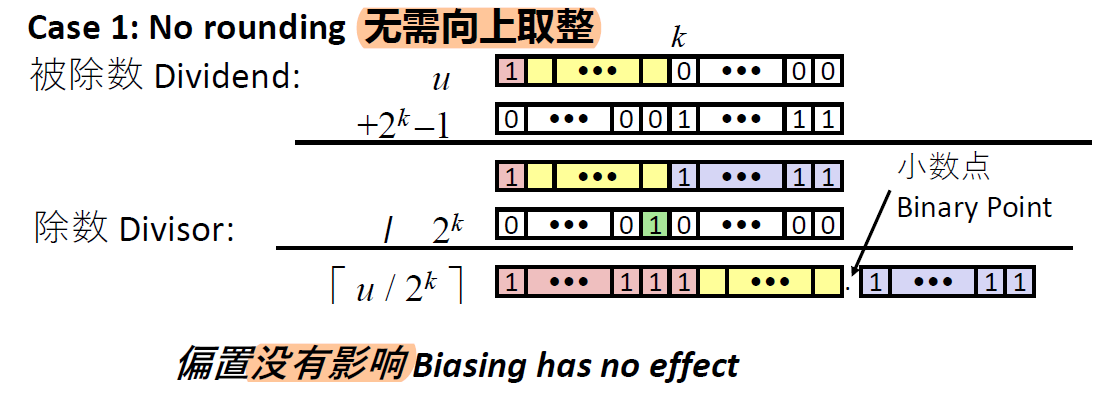
  • 不需要舍入的情况，加上偏置只影响那些被移掉的位 image.png
  • 需要舍入的情况，通过加上$2^k - 1$，会使得第k+1位得到一个进位，从而在后面的移位时向0舍入 image.png

汇编显示

salq  // 左移
shrp  // 逻辑右移
sarq // 算数右移

image.png image.png

有坑

// example 1 死循环
unsigned i;
for (i = cnt-2; i >= 0; i--)
    a[i] += a[i+1];
// 根本不可能小于0

// 正确方法
unsigned i;
// 这里按照无符号比较，当i=-1时就会转成最大的UMax，就会退出循环(即使cnt在Umax时仍然能够正常运行)
for (i = cnt-2; i < cnt; i--)
    a[i] += a[i+1];

// 更好的办法
size_t i;
for (i = cnt-2; i < cnt; i--)
	a[i] += a[i+1];
//数据类型size_t定义为长度为字长的无符号值，与机器有关，可移植性更强


// example 2 隐式类型转换问题
#define DELTA sizeof(int) 
// sizeof(int) 这个结果是unsigned类型的，因此DELTA也是unsigned类型
int i;
// 有符号 - 无符号，会隐式类型转换为无符号类型
for (i = CNT; i-DELTA >= 0; i-= DELTA)

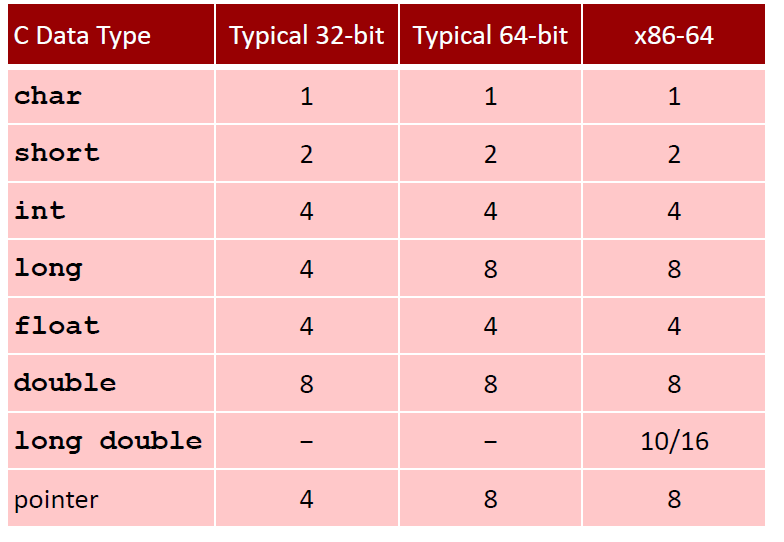
内存中的表示、指针和字符串

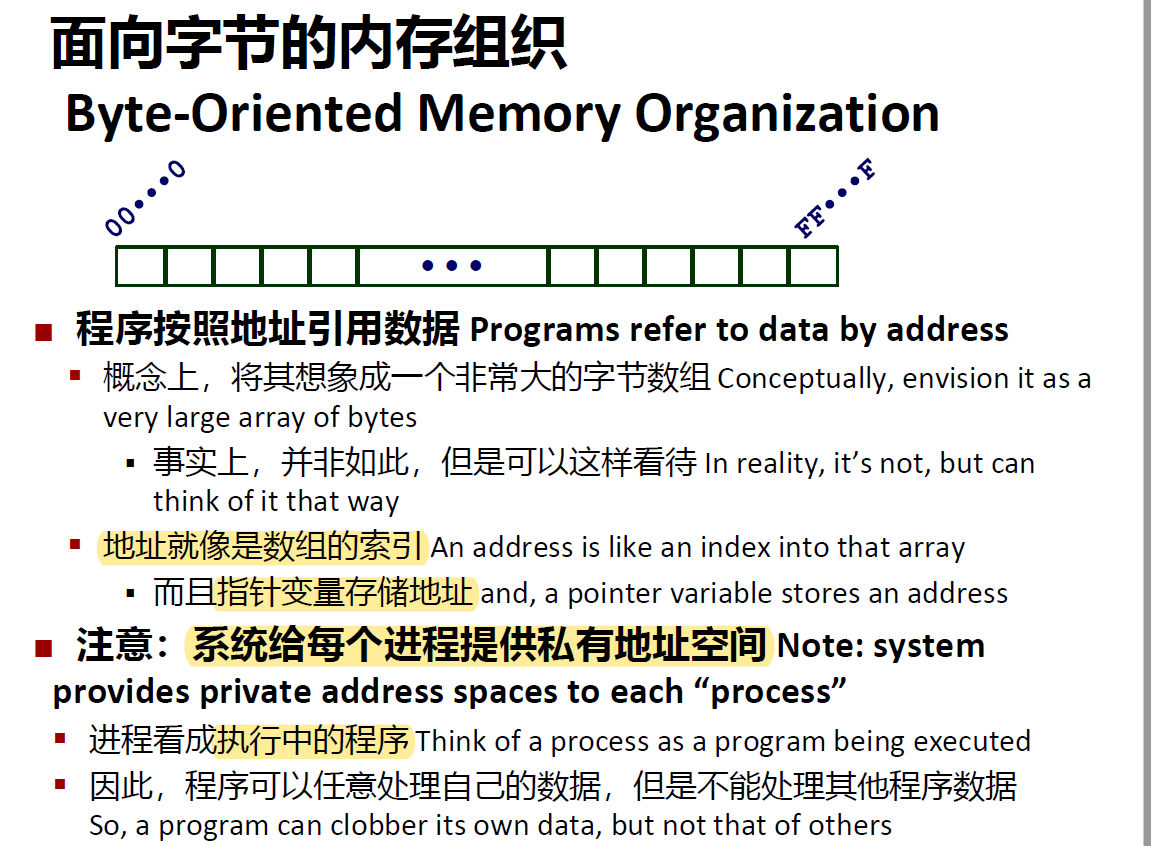image.png 关于字的问题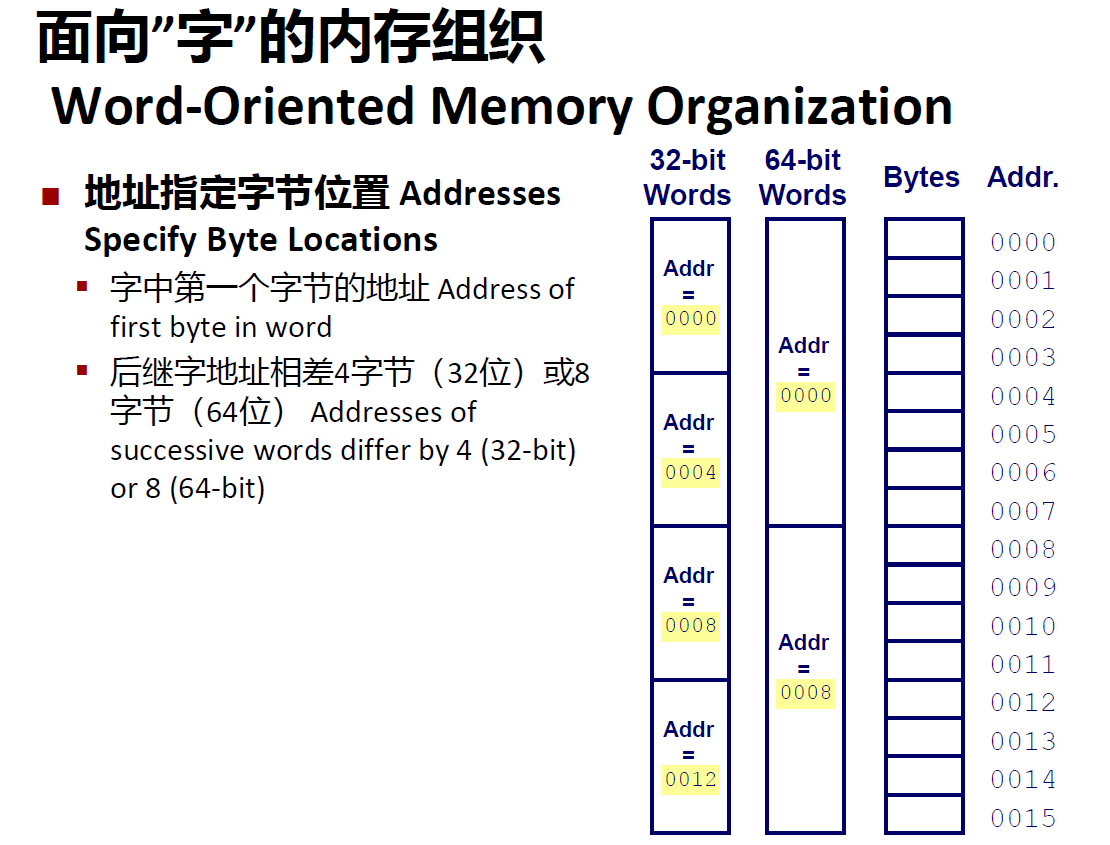： image.png 数据表示： image.png

字节顺序

[!info] 通常来说，大端法更符合日常实际，但更少见

大端法：最低有效字节在最高的地址 小端法：最低有效字节在最低的地址 image.png

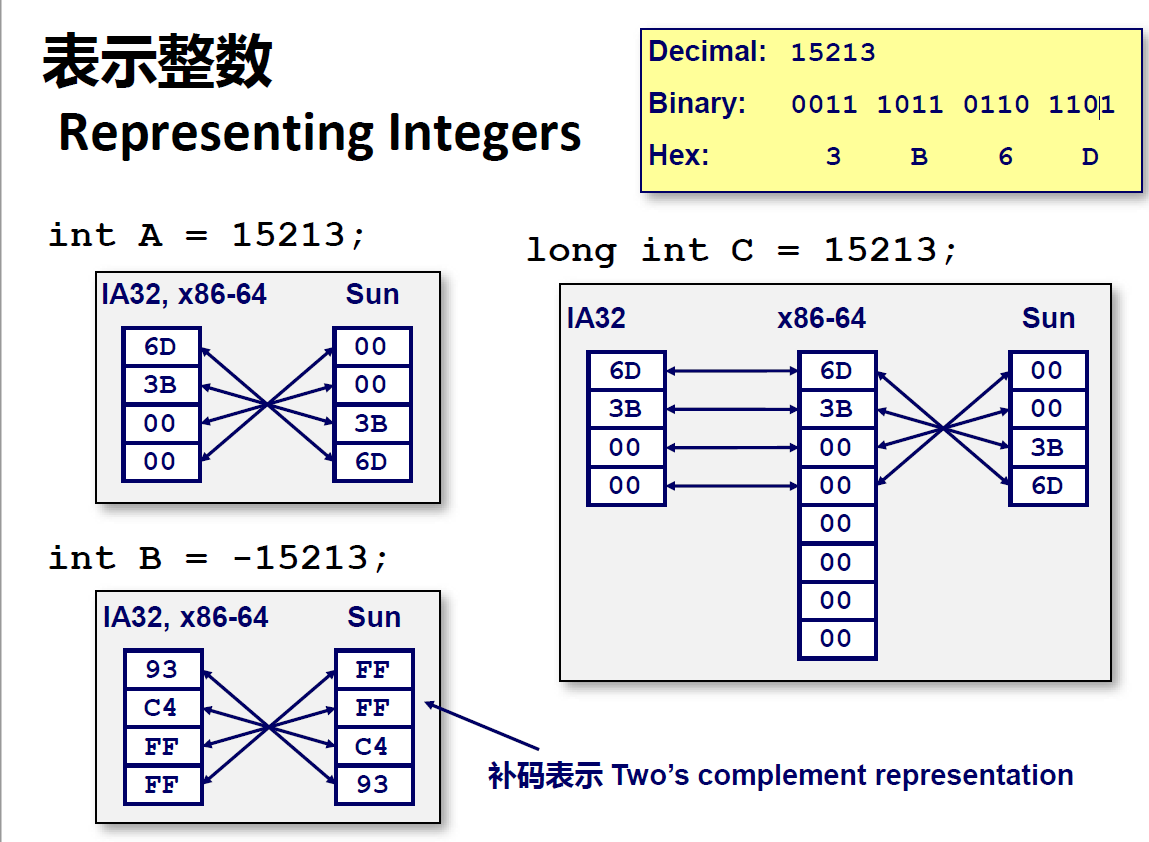
IA32,X86-64是大端，Android,IOS等是小端 image.png

使用强制类型转换检查数据表示

使用无符号字符指针类型pointer允许作为字节数组对待

typedef unsigned char * pointer;

void show_bytes(pointer start, size_t len){
	size_t i;
	for (i = 0; i < len; i++)
	printf("%p\t0x%.2x\n",start+i, start[i]); // %p打印指针，%x打印十六进制
	printf("\n");
}

int a = 15213;
printf("int a = 15213;\n");
show_bytes((pointer) &a, sizeof(int));
/*
int a = 15213;
0x7fffb7f71dbc 6d
0x7fffb7f71dbd 3b
0x7fffb7f71dbe 00
0x7fffb7f71dbf 00
*/

注意字符串的表示

C语言中的字符串用字符数组来代表，每个字符编码成ASCII格式

  • 标准7位字符集编码
  • 字符‘0’编码为0x30(ascii码对应48)
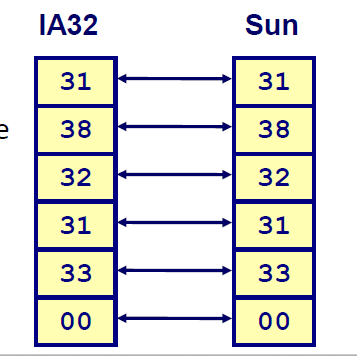
  • 字符串应该以空作为结尾 兼容性:字节顺序不存在问题(无论大端还是小端，都一样的表示) image.png

坑

// 初始化
int x = foo();
int y = bar();
unsigned ux = x;
unsigned uy = y;

// ques
x < 0  -> ((x*2) < 0)  // 错，会溢出
unx >= 0 // 对
x & 7 == 7 -> (x << 30) < 0 // 对，画出位数就好
ux > -1 // 错，会发生隐式类型转换，-1变成unsigned，对应umax
x > y -> -x < -y // 错，如果y为Tmin，那么绝对值仍为Tmin
x * x >= 0 // 错，溢出问题
x > 0 && y > 0 -> x + y > 0 // 错，溢出
x >= 0  -> -x <= 0 // 对
x <= 0  -> -x >= 0 // Tmin情况
(x|-x) >> 31 == -1  // 错，注意0的情况
ux >> 3 == ux / 8 // 对
x >> 3 == x / 8 // 错，注意取整问题
x & (x-1) != 0  // 错，注意0

浮点数

二进制小数

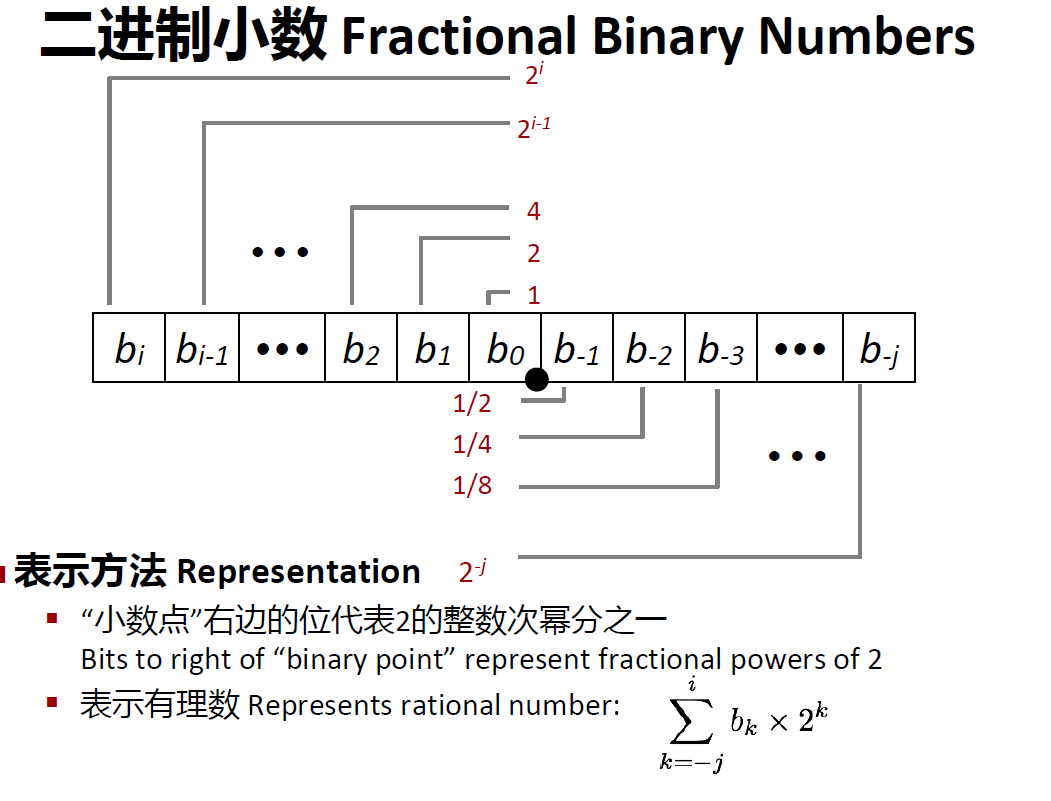image.png 位数对应的是分母，是2的幂次，对应的二进制数是分子 image.png 但使用该方法计算得到的小数有误差，因为这样得到的数是离散的，而小数是连续的： image.png

IEEE浮点数

  • IEEE 754标准
    • 1985年制定作为浮点运算的统一标准
    • 得到所有主流CPU的支持
  • 由数值问题所驱动

浮点表示

\(V=(-1)^s\times M \times 2^E\)

  • 符号位s确定数值是负还是正
  • 尾数M是范围在$[1.0,2.0)$之间的普通小数
  • 指数E是给浮点数指定2的E次幂权重

编码

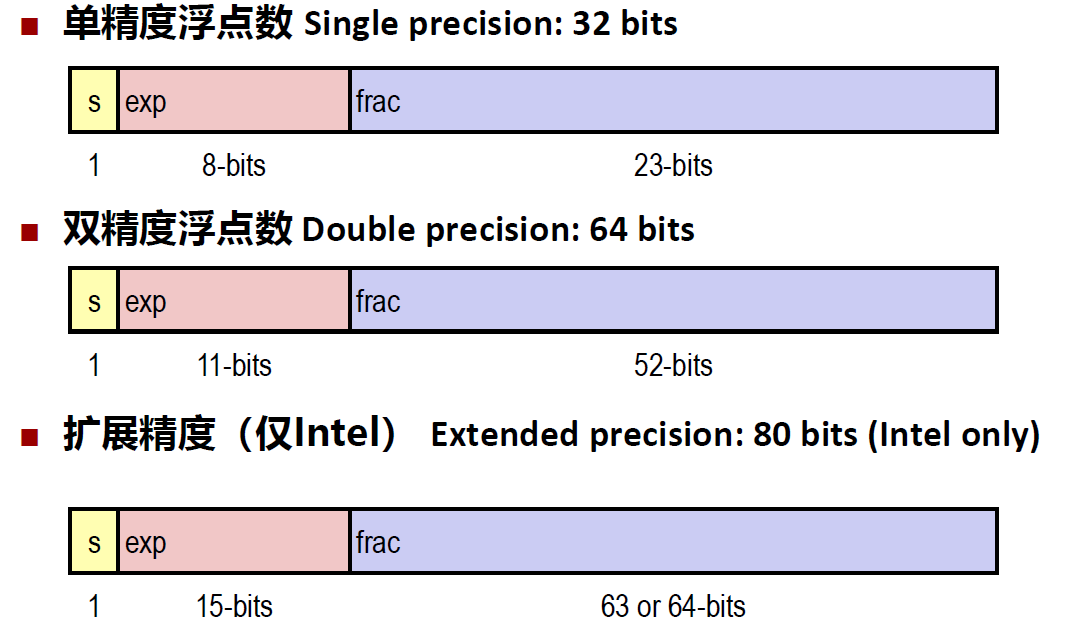
最高位是符号位s exp字段编码E（但不等于E） frac字段编码M（但不等于M） image.png image.png

位向量表示分类

  • 规格化的数
  • 非规格化的数
  • 特殊值

image.png

规格化

当Exp为非全0或者非全1 此时阶码编码E为带偏置的有符号数：\(E=Exp - Bias\) 其中，$Bias = 2^{k-1} - 1$ 因此，此条件下\(\begin{cases}E_{max} = 254(1111\ 1110)-127 = 127\\E_{min} = 1(0000\ 0001)-127 = -126\end{cases}\) 尾数编码M带一个隐含的前导1 当frac全零时值最小Minimum when $frac=000…0 (M = 1.0)$ 当frac全一时值最大Maximum when $frac=111…1 (M = 2.0 – ε)$ 表示范围： image.png 正数范围：$[2^{-126}, 2 \times 2^{127})$，负数范围：$(-2 \times 2^{127}, -2 ^{-126}]$ 注意，因为frac全1时候，$M=2.0-\epsilon$，虽然很接近但是并没有到2，所以是半开半闭区间

示例：单精度浮点数 image.png 但同样不是精准的 image.png

非规格化

条件：Exp为全0

  • 阶码值：$E = 1 - Bias$，这里作了特殊处理，不是0-Bias
  • 尾数编码M为隐含的一个前导0 此时$M=f$，即M的取值范围为$[0,1.0)$(因为最大是$1 - \epsilon$)

特殊情况：表示0 exp = 000...0, frac = 000...0 代表0值，但注意由于有符号位的存在，所以会出现+0和-0

此时表示的范围区间：$(-2^{-126}, 2^{-126})$，非常巧妙地将规格化数和规格化数范围联系在一起 image.png

性质：

  • 逐渐溢出：非规格化数一点点逐渐变大，最大值平稳衔接规格化数的最小值
  • 密集分布：越靠近0越密集，越靠近无穷越稀疏

特殊值

  • 条件：Exp为全1
  • 情况1：frac = 000…00
    • 代表无穷大
    • 此时为溢出
    • 正负均如此
    • E.g., $1.0/0.0 = −1.0/−0.0 = +\infty$, $1.0/−0.0 = −\infty$
  • 情况2：$frac \not = 000…0$
    • 不是一个数
    • 代表无法确定数值的情况
    • E.g $\infty - \infty$, $\infty \times 0$

image.png

C语言的浮点数

image.png image.png

特殊性质

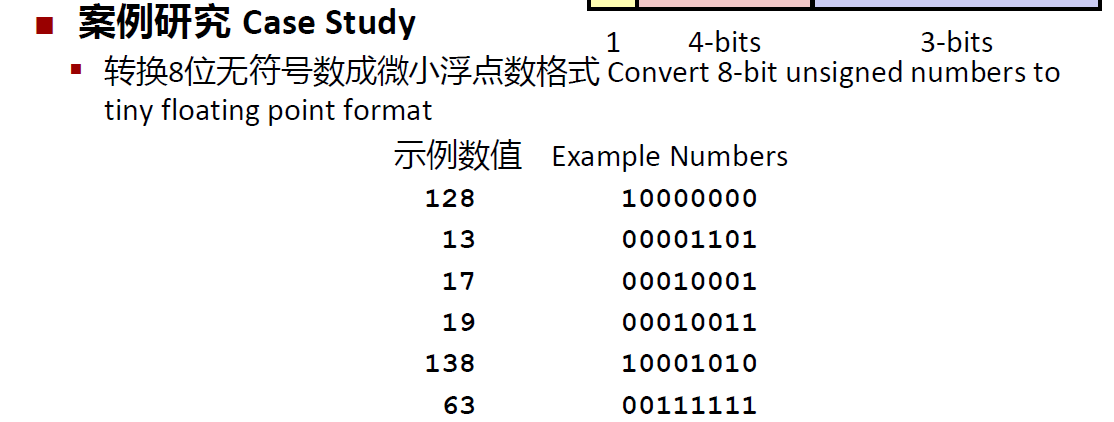
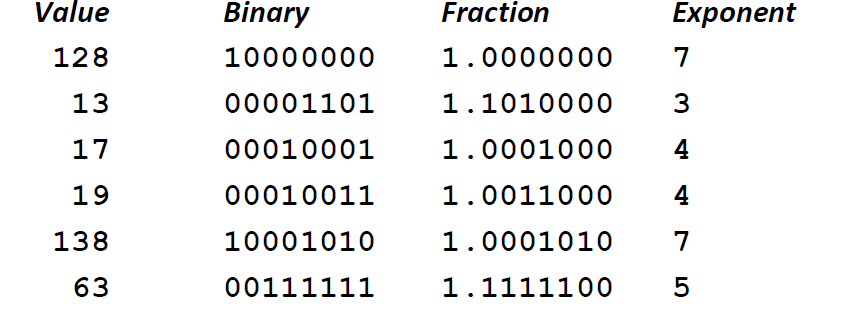
以8位浮点数为例子 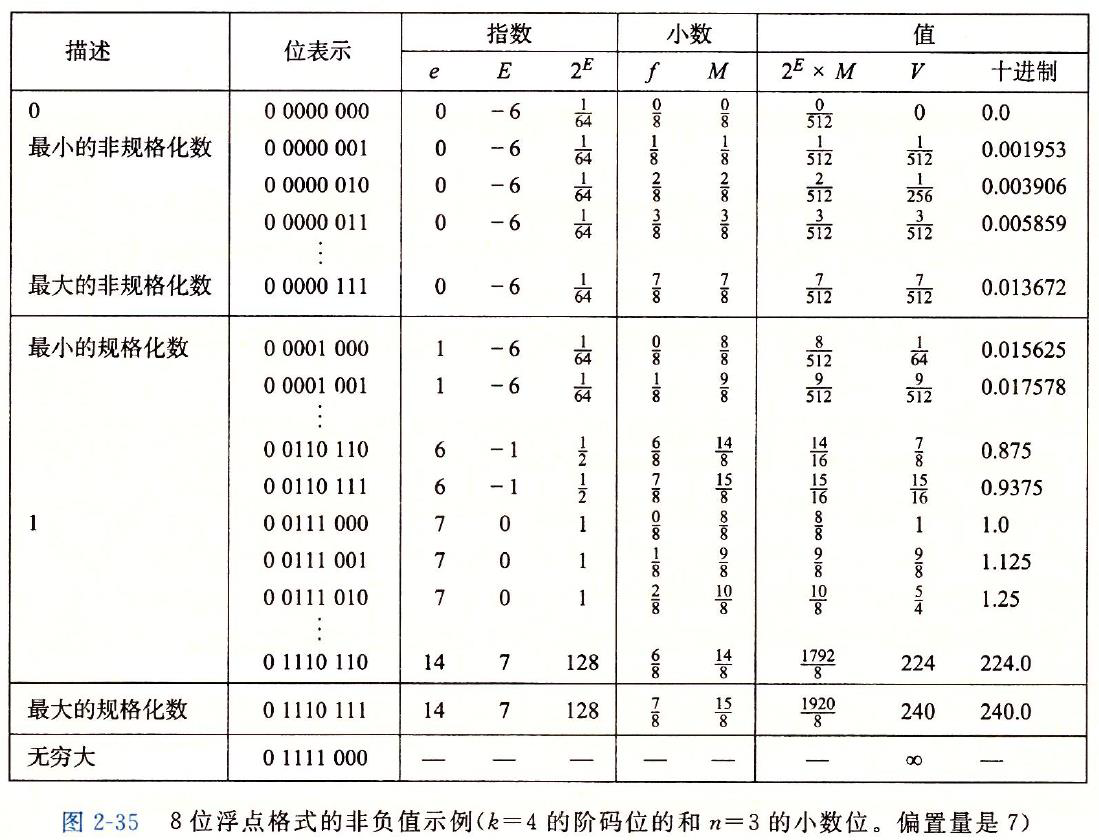image.png image.png 发现

  • 最小规格化数和最大非规格化数之间的平滑转变，通过非规格化数$E=1-Bias$得到，补偿了非规格化数尾数没有隐含的1
  • 即使将非负值看成无符号数，其也是升序排列的
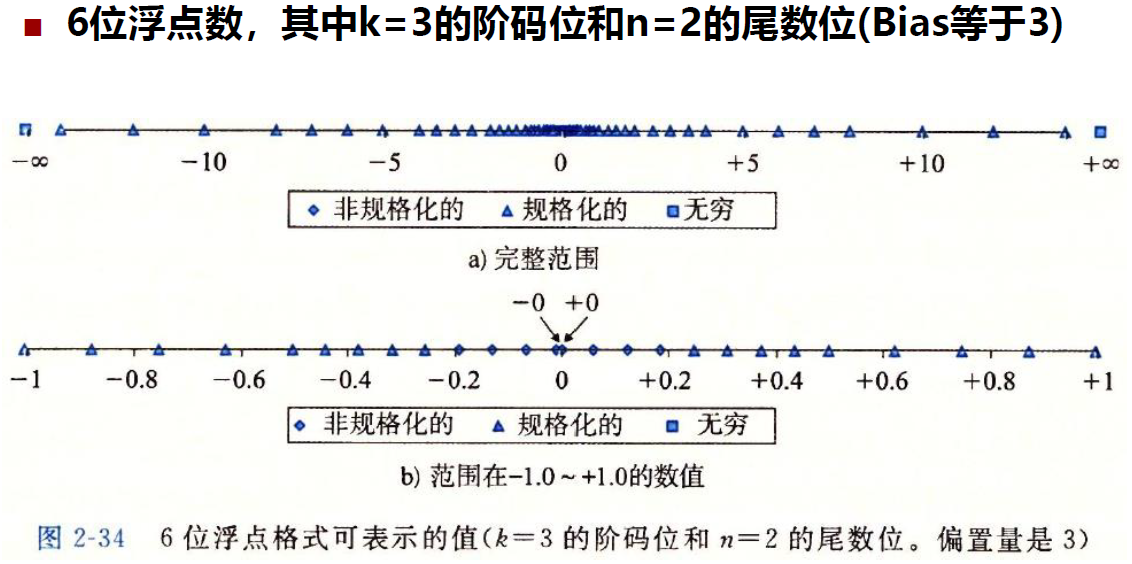
  • 值的分布：越接近零分布越密集 eg. 6位浮点

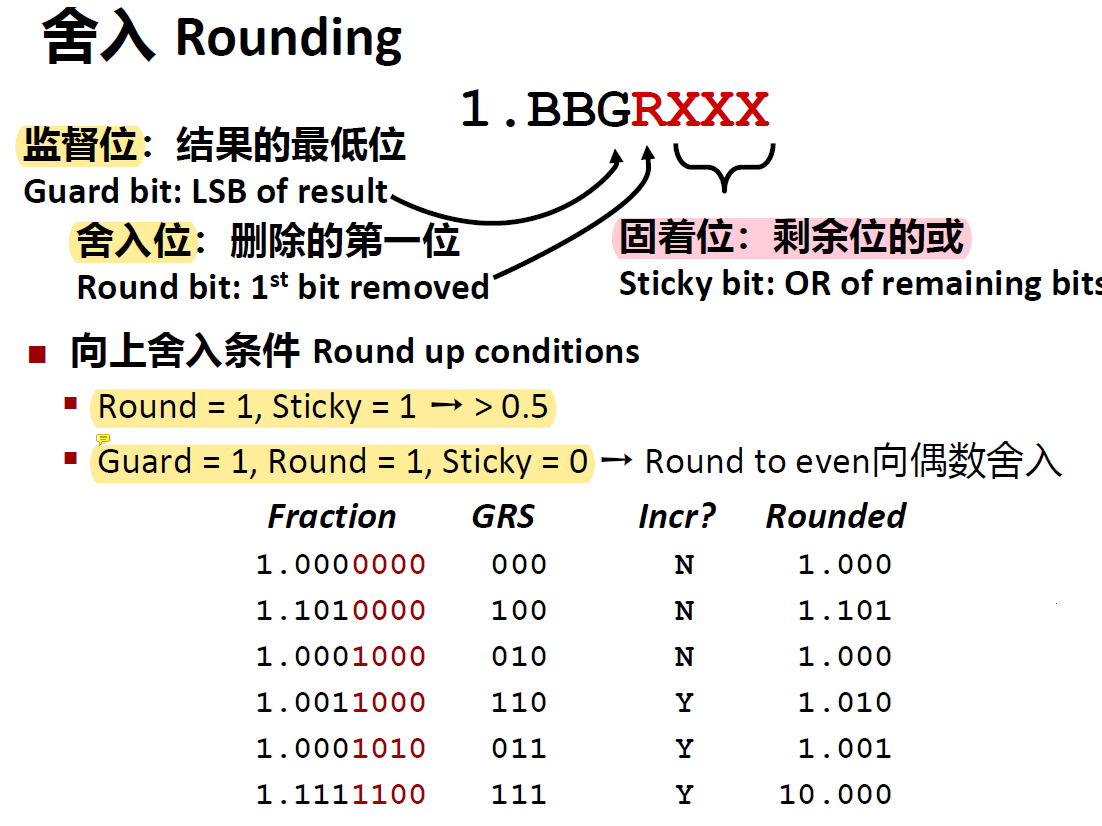
image.png

舍入

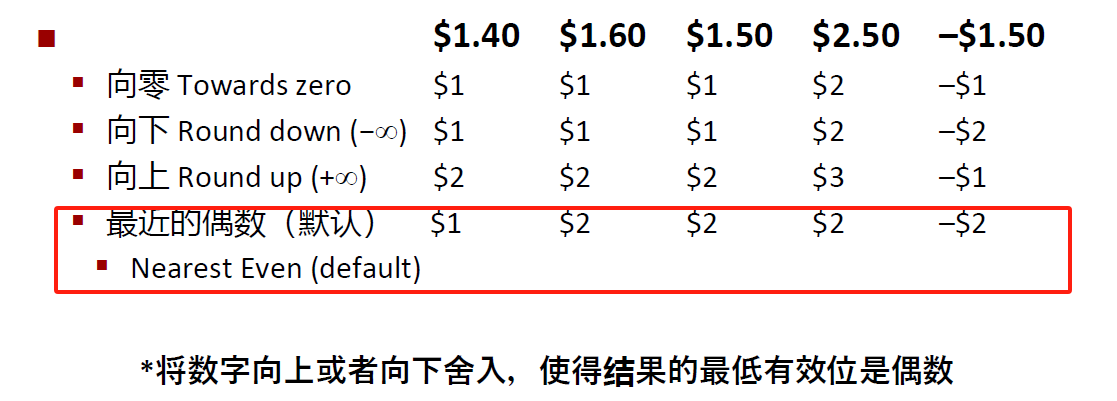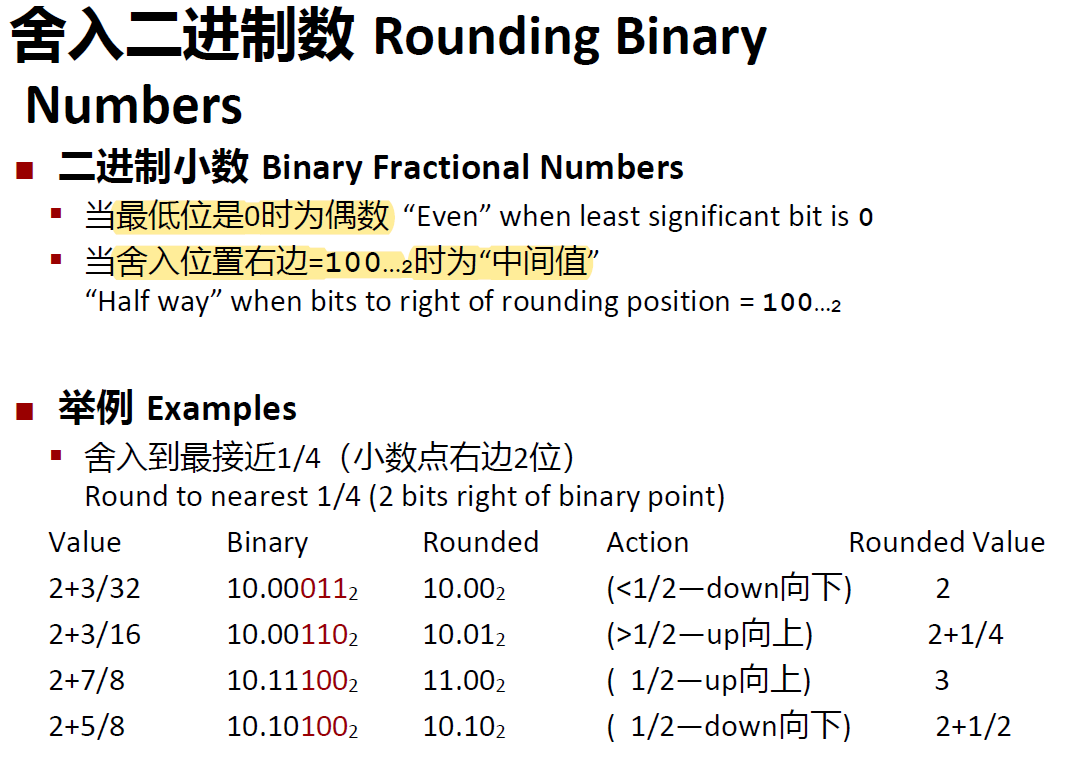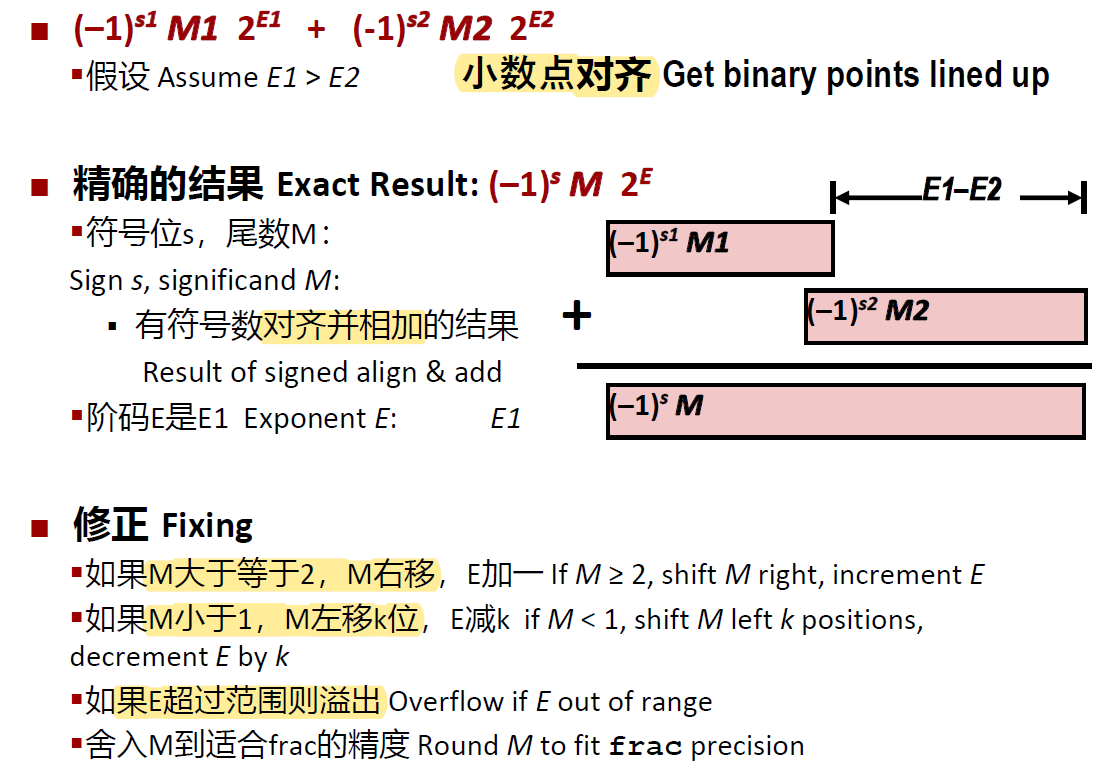image.png 当正好位于两个可能值中间时，舍入以便最低位是偶数 适用于其它小数位/比特位位置 image.png 判断是否需要舍入的另一种方法(虽然感觉没太大必要)： image.png

浮点运算

image.png

浮点加法

image.png 用小阶码对大阶码 image.png

浮点乘法

image.png

C语言中的浮点数

image.png

转换

doube/float -> int

  • 截断尾数部分，向0舍入
  • 当超过范围时或者NaN时候没有定义：一般设置为TMin

int -> double

  • 因为double尾数位置够长，所以可以精确转换

int -> float

可以转换，但是需要舍入(2.49提到float能准确表示的最大整数值为$2^{24}$)

创建浮点数：

  • 用前导1规格化尾数
  • 舍入以适合尾数位
  • 后规格化以处理舍入的影响 image.png
规格化

设置小数点以便数值格式为1 调整所有位得到前导1 Adjust all to have leading one ▪ 尾数左移，阶码减1 ▪ 尾数右移，阶码加1 image.png

后规格化

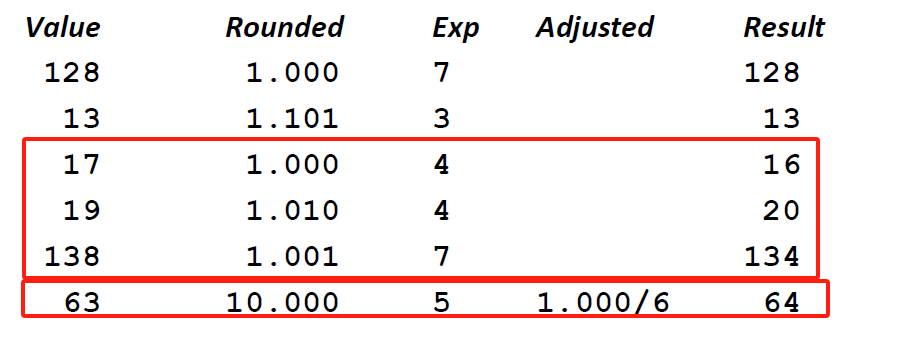
舍入可能导致溢出 通过右移一次进行处理同时阶码加一 image.png

坑

image.png

  • 前四个类型转换需要注意数据表示范围和舍入精度问题，float不一定能装下int和double，但是double可以将两个都装下
  • 浮点数符号只需要改变符号位
  • 浮点数具有单调性(即使溢出到正无穷也大于0)
  • 隐式类型转换
  • 最后一个是精度问题