计算机某些不可忽略的事实
int不是整数,float不是实数
- $x^2$总是大于0吗?
#include<bits/stdc++.h>
int main(void){
float x1 = 1e19; // 1e38
std::cout << x1 * x1 << '\n';
float y1 = 50000; // 2.5e+9
std::cout << y1 * y1 << '\n';
float x3 = 1e20; // inf
std::cout << x3 * x3 << '\n';
int x2 = 50000; // -1794967296
std::cout << x2 * x2 << '\n';
int y2 = 40000; // 1600000000
std::cout << y2 * y2 << '\n';
return 0;
}
发现对于float类型来说,确实结果总是大于0(对于超过表示范围直接输出inf)
但是对于int类型,如果结果超过了其能表示的最大值,那么会出现溢出,结果变成负数
- 加法结合律总是成立吗?
- 对无符号和有符号整数正确
- 浮点数:
#include<bits/stdc++.h>
int main(void){
float x1 = 1e19; // 1e38,double也如此
std::cout << (x1 - x1) + 3.14 << '\n'; // 3.14
std::cout << x1 - (x1 + 3.14) << '\n'; // 0
return 0;
}
对于浮点数,由于其表示方式是“符号位+阶码+尾码”形式,因此对于位数相差过多的数会因为舍入产生误差(对阶过程中因为需要小阶对大阶,所以阶码需要一直加,然后尾码在不断右移时丢失了,计组的知识了)
计算机算数性质
-
不会产生随机值(这里说的不是
random的伪随机问题,而是计算机的算数运算一般情况下符合正常规则,不会有异常) - 算术运算有重要的数学性质 - 不能假设所有“通常”的数学性质成立
- 整数运算满足“环”性质(交换率、结合率和分配律成立)
- 浮点运算满足“按序”性质(满足单调性)
- 需要理解哪些抽象适用于哪些上下文
你必须懂汇编语言

存储器很重要
随机访问存储器是一种非物质抽象
- 内存不是无限界的
- 它必须进行分配和管理
- 很多应用都受内存空间的限制
- 存储器性能并不一致
- 高速缓冲和虚拟存储器可以显著影响程序性能
- 根据存储系统特点调整程序可以导致很大速度改进
- 内存引用错误特别有害
- 在时间和空间上都是影响滞后的
#include<iostream>
using namespace std;
typedef struct{
int a[2];
double d;
}struct_t;
double fun(int i){
volatile struct_t s;
s.d = 3.14;
s.a[i] = 1073741824;
return s.d;
}
int main(void){
for(int i = 0; i <= 6; i++){
cout << "fun(" << i << ") = " << fun(i) << endl;
}
return 0;
}
/* linux 运行结果
fun(0)= 3.140000000000
fun(1)= 3.140000000000
fun(2)= 3.139999866486
fun(3)= 2.000000610352
fun(4)= 3.140000000000
fun(5)= 3.140000000000
*** stack smashing detected ***: terminated
Aborted
*/
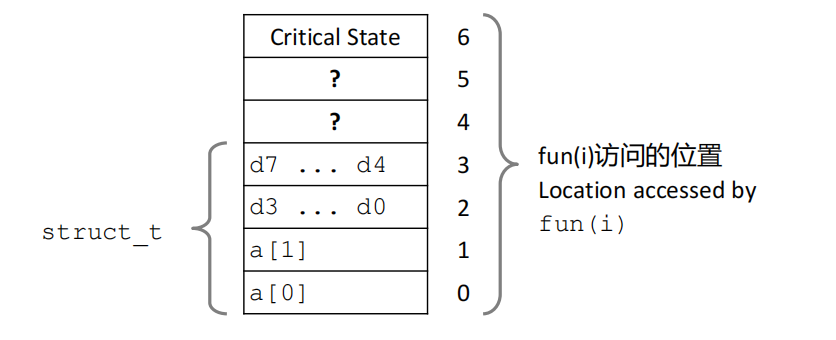
如图所示,因为a数组只分配了两个地址,一个地址4个字节,而double分配了8个字节,所以当i=2的时候,a[i]会修改double的前4个字节,而i=3同理。
对于十进制的1073741824转换为2进制为0100 0000 0000 0000 0000 0000 0000 0000
对于十进制的3.14,转换为2进制为0100 0000 0100 1000 1111 0101 1100 0010
这里涉及到的是double的IEEE标准:1位符号位 + 11位阶码位 + 52位尾码位,以及大端表示
- 当覆盖了
d0-d3实际上是将值覆盖了部分尾码,因为0100影响的很小,结果没有太大的改变 - 当覆盖了
d4-d7实际上覆盖的是符号位+所有阶码位+一部分尾码位,使得前面的值只有0100...0000,然后因为阶码是移码表示的,所以变成了$2^{2^11 - (2^11 - 1)}=2$,尾数留下了一小部分,使得结果含有无规律的小数
内存引用错误 Memory Referencing Errors
- C语言和C++不提供任何内存保护
- 数组引用超界
- 不合法的指针值
- 分配和释放内存滥用
- 可能导致严重的错误
- 是否错误有任何影响取决于系统和编译器
- 在远处产生影响
- 破坏的对象逻辑上和访问的对象毫不相关
- 错误的效果第一次观察到可能距离产生的时间很长
- 这种情况应该如何处理?
- 采用Java、Ruby、Python、ML等编程
- 理解可能会发生什么相互影响
- 使用或开发工具来检测引用错误(例如Valgrind)
性能不仅仅是渐进复杂度
- 常数因子也很重要
- 而且甚至精确的操作计数都不能预测性能
- 很容易发现10倍性能差异取决于如何编写代码
- 必须在多个级别进行优化:算法、数据表示、过程和循环
- 必须理解系统才能优化性能
- 程序是如何编译和执行的
- 如何测量程序性能和识别瓶颈
- 如何改进性能同时不破坏代码的模块性和通用性
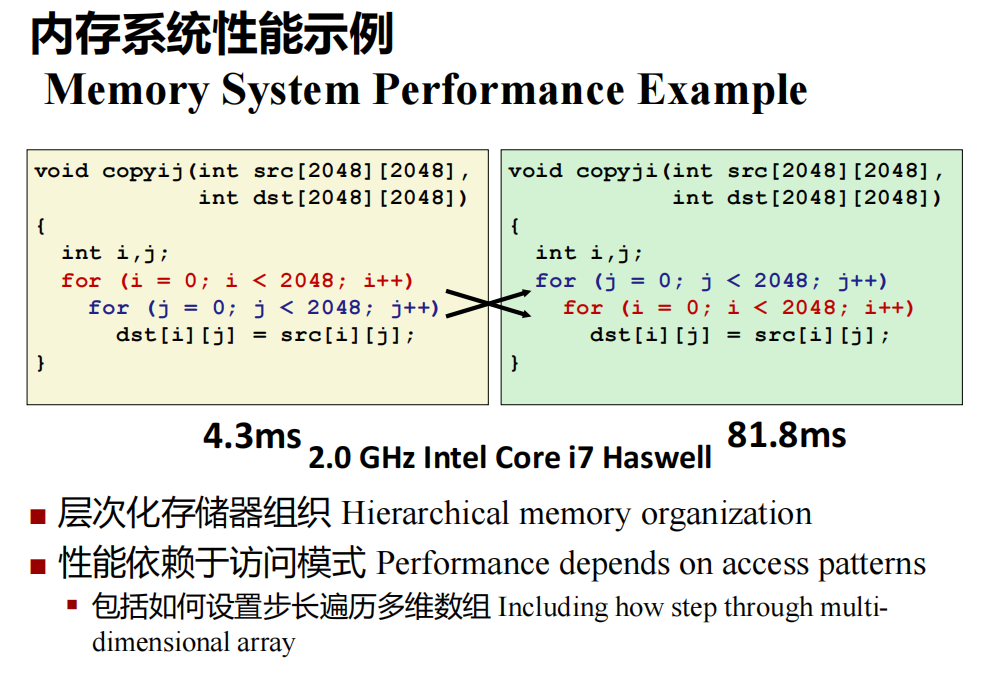
在计算机中,多维数组是按行存储的,因此先访问行再访问列时间消耗会比先访问列再访问行快得多
计算机不仅执行程序还做更多的事情
- 计算机需要完成数据输入和输出
- I/O系统对程序的可靠性和性能至关重要
- 计算机通过网络进行彼此通信
- 很多系统级问题由于网络引起
- 自治进程的并发操作
- 处理不可靠的传输介质
- 跨平台的兼容性
- 复杂的性能问题
- 很多系统级问题由于网络引起
信息是比特位+上下文
hello.c的ASCII文本表示
 信息由一串比特位表示,区分不同数据对象的是上下文
信息由一串比特位表示,区分不同数据对象的是上下文
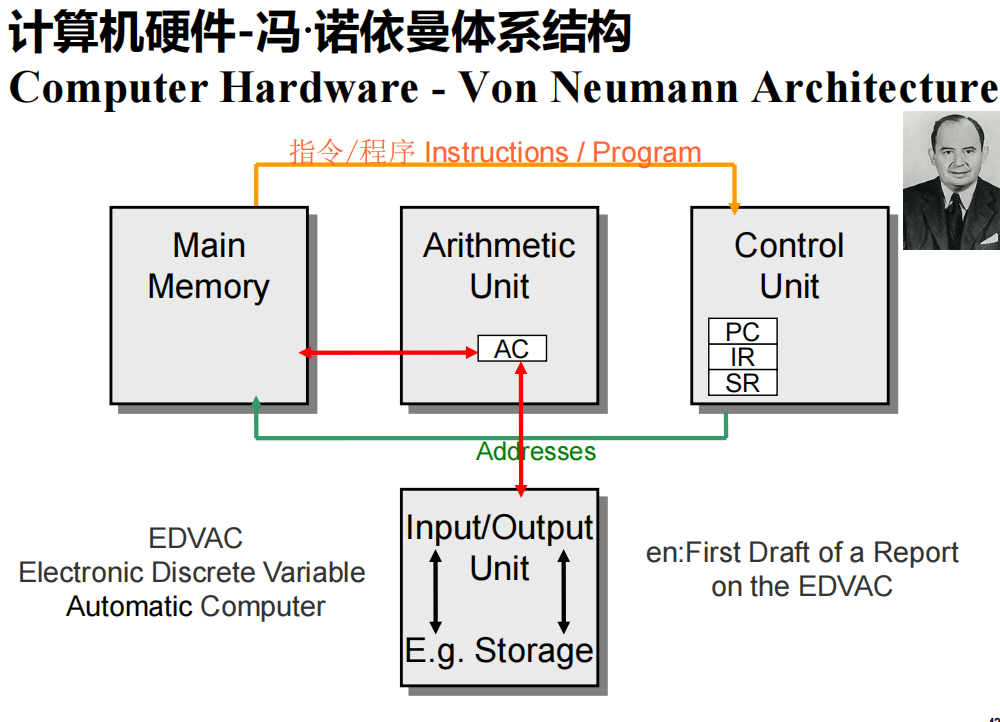
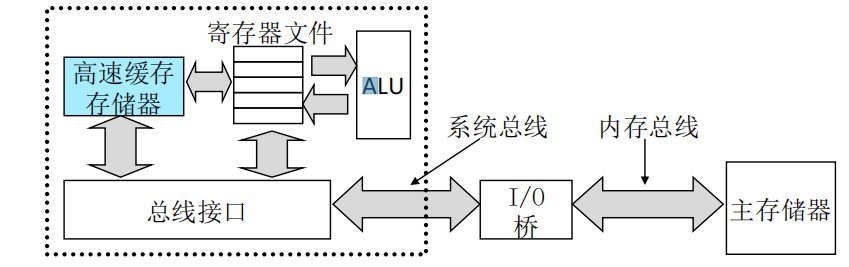
硬件-冯·诺依曼体系结构
编译过程
编译系统
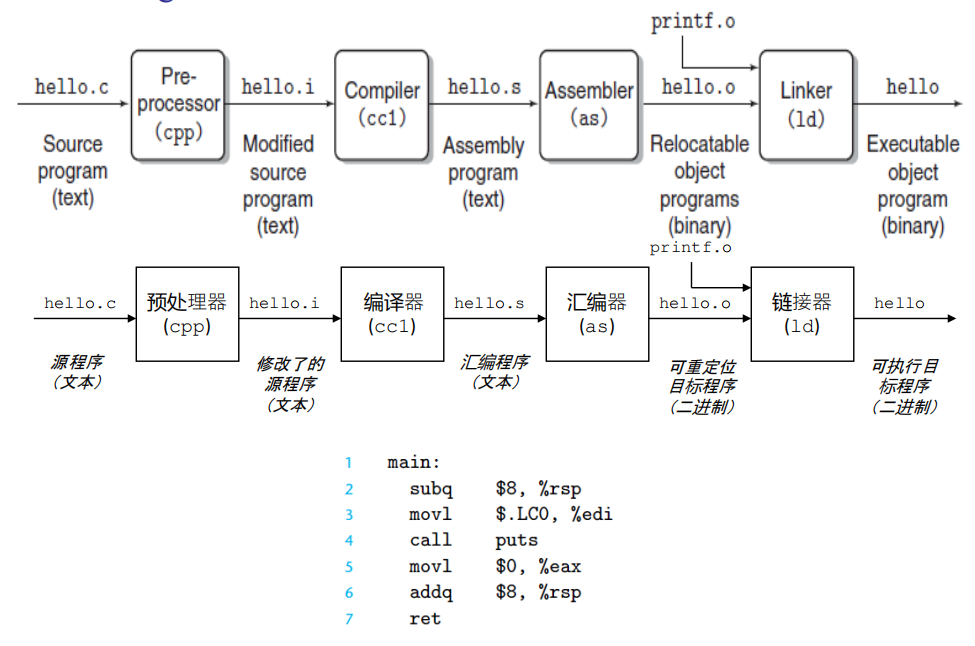
- 预处理:导入include的头文件,插入到程序文本,生成
hello.i - 编译:通过编译器将hello.i翻译成汇编语言
hello.s - 汇编:将hello.s翻译成机器语言形式,并打包成可重定位目标程序
hello.o(二进制文件) - 链接:将其余目标文件(如
printf.o)合并到hello.o程序中,使得可以被加载到内存中并执行
处理器读并解释存储在内存中的指令
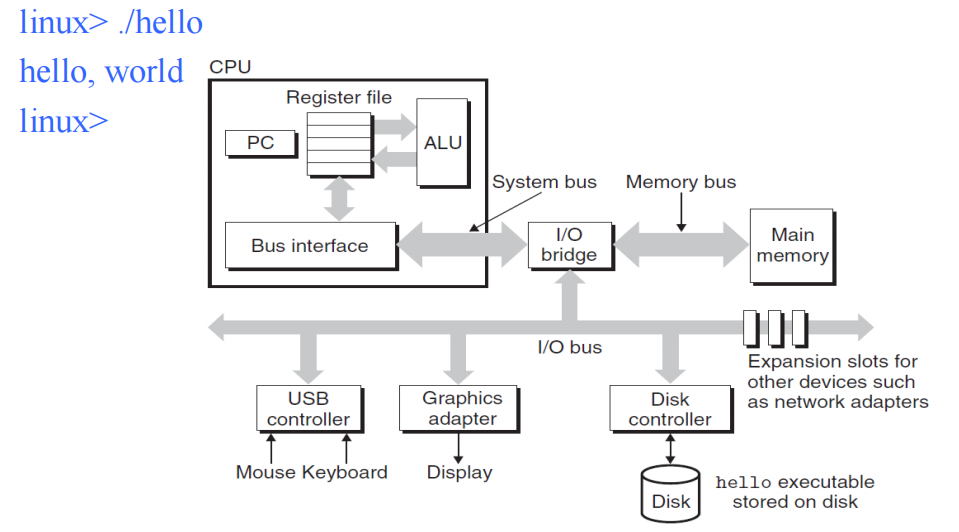
hello的运行
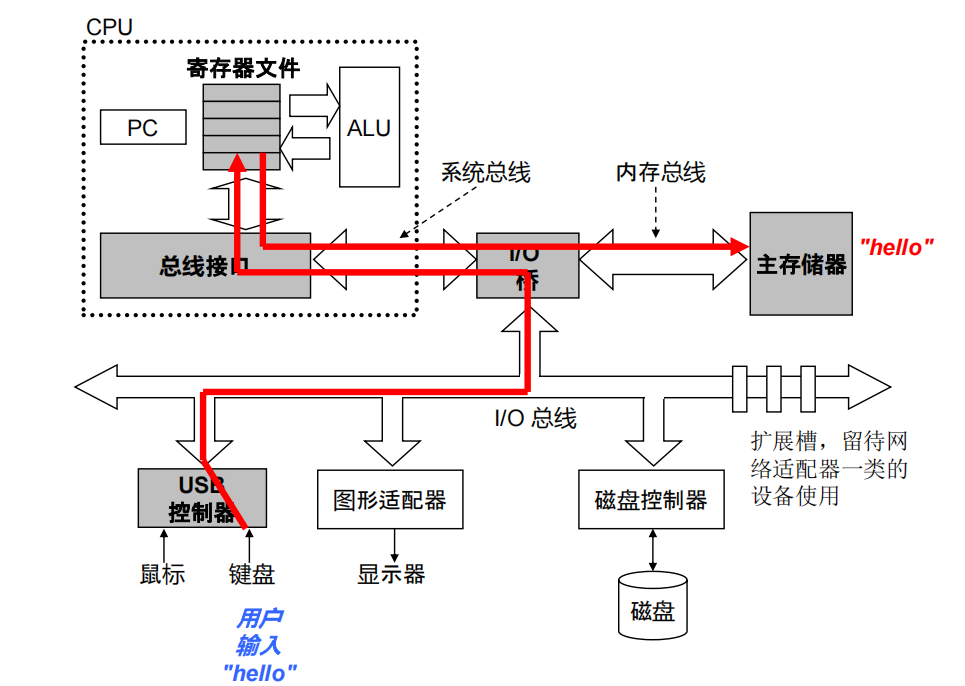
- 用户输入”hello”,指令通过总线和IO桥进入CPU,CPU再让主存存储”hello”
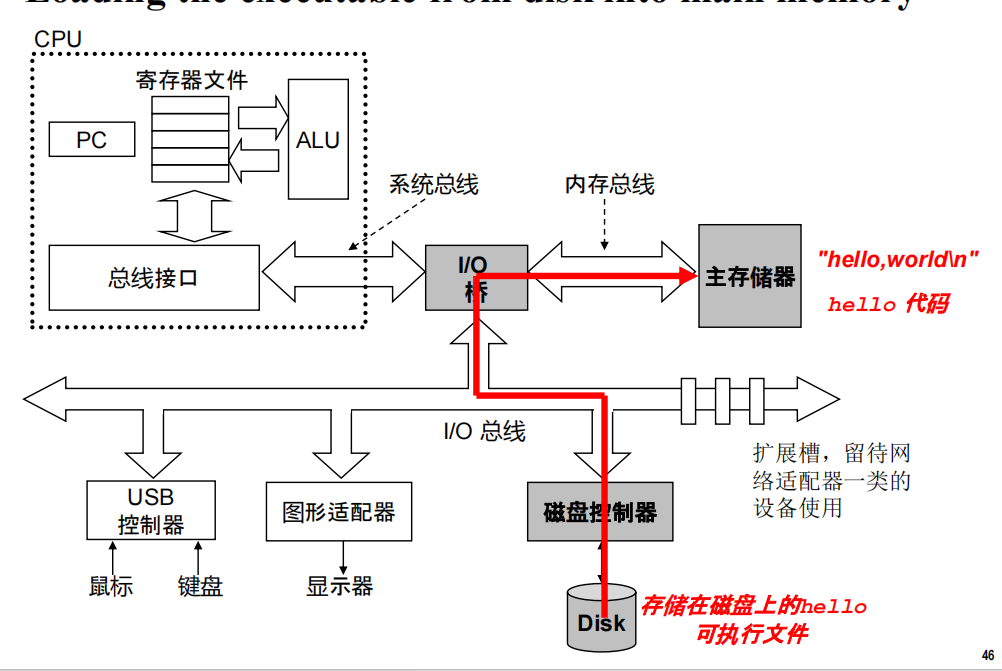
- 利用直接存储器DMA将数据(可执行文件)从磁盘加载到主存中
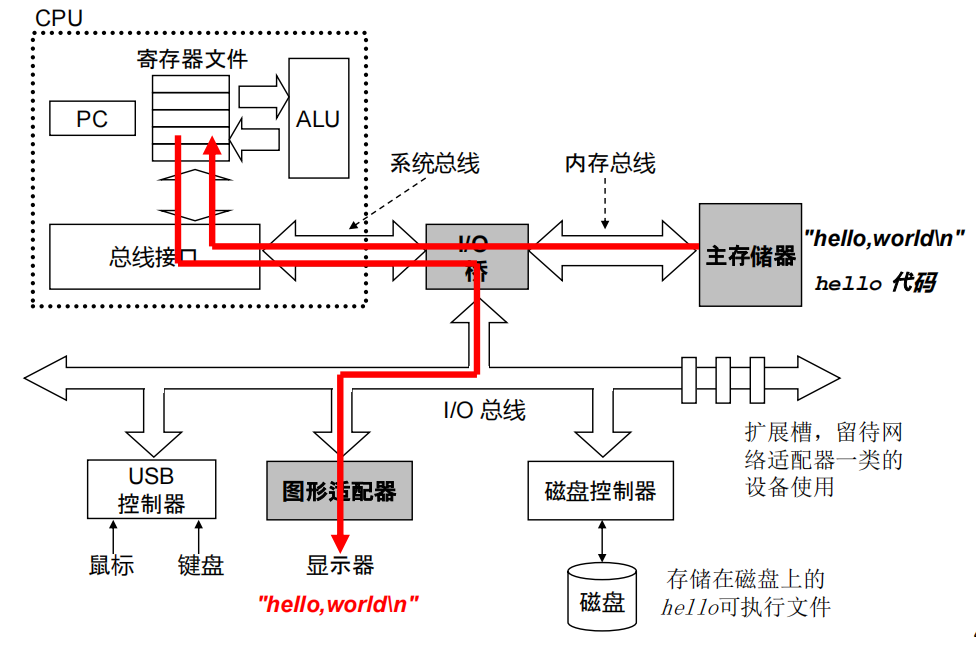
- 将输出字符串从内存写入显示器
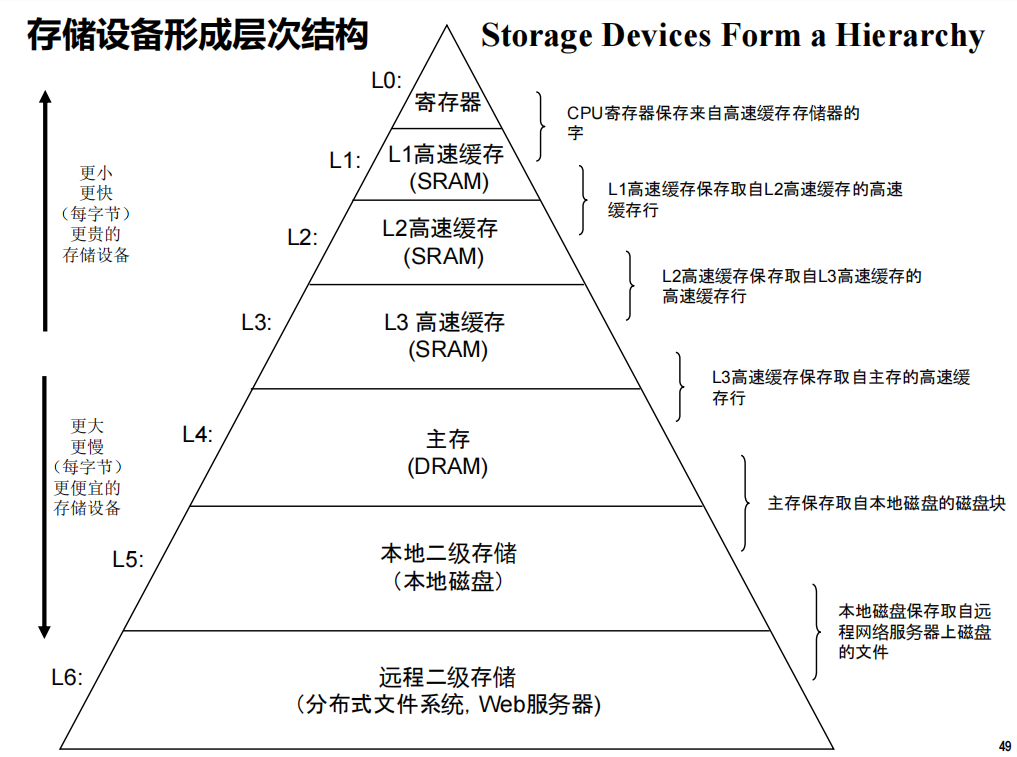
高速缓存至关重要
- 处理器和内存速度鸿沟持续增大
- 更小和快速的存储设备称为cache存储器(简称cache)
- 用称为静态随机访问存储器硬件技术实现
操作系统管理硬件

两个基本目的
- 保护硬件防止被失控的应用误用
- 给应用提供简单统一的机制操作复杂和差异巨大的低层硬件设备
三大抽象
文件——I/O设备抽象
- 文件就是字节序列
- 每个I/O设备都可以看成是文件
- 输入输出都是通过系统函数调用读写文件来实现的
- 同一个程序可以在使用不同磁盘技术的不同系统上运行
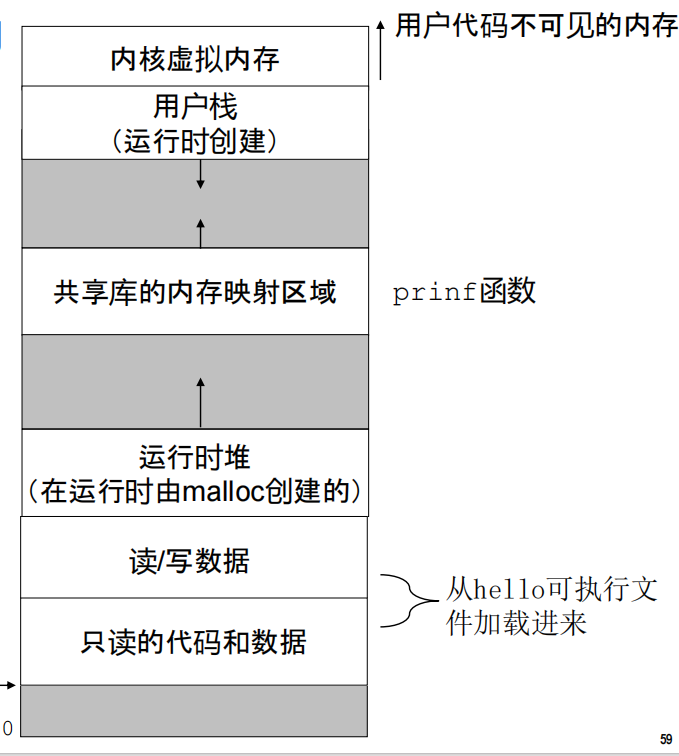
虚拟内存——I/O+主存
- 每个进程有同样一致的内存视图,称为进程的虚地址空间
- 虚拟内存 是一个抽象概念,它为每个进程提供了一个假象,即每个进程都在独占地使用主存。
- 每个进程看到的内存都是一致的,称为虚拟地址空间
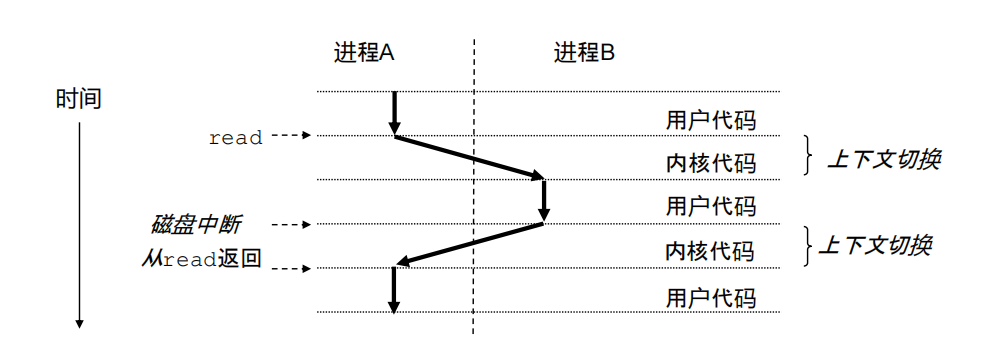
进程——I/O+主存+处理器
进程是操作系统对运行程序的抽象
虚拟机——整个计算机抽象
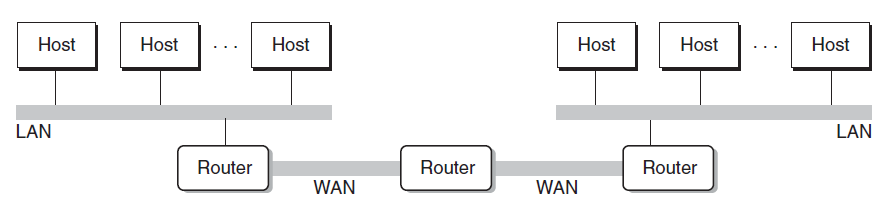
系统之间使用网络通信
- 网络也是一种I/O设备,计算机之间使用网络进行连接

重要主题
阿姆达尔定律 Amdahl’s Law
对系统的某个部分加速时,其对系统整体性能的影响取决于该部分的重要性和加速程度 \(S = \frac{T_{old}}{T_{new}}=\frac{1}{(1-\alpha) + \frac{\alpha}{k}}\)
- 该部分时间占比为α
- 该部分性能改进提高k倍
必须提升在总体系统中占比非常大的部分的速度,才能提高总体性能 当$k \to \inf$,那么这部分时间就可以忽略不计,得到\(S_{\infty}=\frac{1}{1-\alpha}\)
并发和并行
- 并发指同时具有多个活动的系统这个通用概念
- 并行指用并发使系统运行更快
- 并行可以在计算机系统的多个抽象层次上运用
三个层次
线程级并发
- 在进程抽象基础上,多个程序同时执行,导致并发
- 使用线程可以在单一进程中有多个控制流
- 从单处理器系统到多处理器系统,最近多核和超线程
- 超线程称为同时多线程,是一项允许单一CPU执行多个控制流的技术
- 要求程序必须以多线程方式编写
指令级并行
- 现代处理器可以一次执行多条指令,称为指令级并行
- 流水线的使用,接近一个时钟周期一条指令的执行速率
- 比一个周期一条指令更快的执行速率,称为超标量处理器
单指令多数据流并行
- 单条指令引起并行执行多个操作
- 某些编译器尝试自动从C程序抽取SIMD并行性
- 自己使用编译器支持的特殊向量数据类型编写程序






