2024-10-28-聚类分析

2024-10-28

虽然是课上第一次学(噢不对，应该是在素红奶奶课上第一次学)，但实际上之前已经学过很多次，现在对其数学原理进行进一步分析：

聚类分析属于非监督分类,也就是说基本上无先验知识可依据或参考。 聚类分析根据模式之间的相似性对模式进行分类,对一批没有标出类别的模式样本集,将相似的归为一类,不相似的归为另一类。

相似性

对于特征向量$\mathbf{X} = [x_{1},x_{2}, \dots x_{n}]^T$，将特征空间中向量与向量间的距离作为模式相似性的一种测量方法。以“距离”作为模式分类的一种依据(考)。除此以外还有基于密度的测量等方法。

教材主要介绍的是基于距离的聚类，故以下内容均在此前提下展开

聚类分析也会与数据的分布有关，如果数据是成多簇分布的，那么容易用距离函数进行分类；如果数据均在同一簇，则难以聚类分析

相似性测度（距离测量）

欧氏距离

\[D(\mathbf{X_{i}},\mathbf{X_{j}})= \vert \vert \mathbf{X_{i}} - \mathbf{X_{j}} \vert\vert = \sqrt{ (\mathbf{X_{i}-\mathbf{X_{j}}})^T(\mathbf{X_{i}-\mathbf{X_{j}}}) }\]
  • 注意由于存在量纲的影响，需要对数据进行标准化，可以统一成标准正态分布或以下形式：
\[\hat{x_{i}} = \frac{x_{i}}{\sum_{i=1}^{N}x_{i}}\]

马氏距离

![f166523c9289ebdce0b5757b0345ae5.png 500](https://hjk-image.oss-cn-shenzhen.aliyuncs.com/image/202410281108758.png)

常用平方形式表示，设$\mathbf{X}$为模式向量，$\mathbf{M}$为某类模式的均值向量，$\mathbf{C}$为该模式总体的协方差矩阵，则马氏距离定义为 \(D^2 = (\mathbf{X}-\mathbf{M})^TC^{-1}(\mathbf{X}-\mathbf{M})\)

其中，$\mathbf{C}$的计算方式为： \(\begin{aligned} \mathbf{C}=&E\{(\mathbf{X-M})(\mathbf{X-M})^T\}=E\begin{bmatrix} (x_{1}-m_{1})\\(x_{2}-m_{2})\\ \vdots \\ (x_{n}-m_{n}) \end{bmatrix}[(x_{1}-m_{1})\quad (x_{2} - m_{2}) \cdots (x_{n}-m_{n})] \\ = &\begin{bmatrix} &E(x_{1}-m_{1}) (x_{1}-m_{1}) &\cdots &E(x_{1}-m_{1}) (x_{n}-m_{n}) \\ &\vdots &\ddots &\vdots \\ &E(x_{n}-m_{n}) (x_{1}-m_{1}) &\cdots &E(x_{n}-m_{n}) (x_{n}-m_{n}) \end{bmatrix} \\ = &\begin{bmatrix} &\sigma_{11}^2 &\cdots &\sigma_{1n}^2\\ &\vdots &\ddots &\vdots \\ &\sigma_{n1}^2 &\cdots &\sigma_{nn}^2 \end{bmatrix} \end{aligned}\)

马氏距离的优点是排除了模式样本之间的相关性影响(考)。 例如我们取一个模式特征向量,可能其中有九个分量反映的是同一特征$A$,而只有一个分量反映特征$B$,这时如用欧氏距离计算,则主要反映了特征$A$,而用马氏距离计算则可避免这个缺点。 当$\mathbf{C}$为单位矩阵$\mathbf{I}$时,马氏距离等同于欧氏距离。

明氏距离

\(D_{m}(\mathbf{X_{i},\mathbf{X_{j}}})=\left[ \sum_{k=1}^{n}\vert x_{ik}-x_{jk}\vert^m \right]^{1/m}\) 当$m=2$时，明式距离即为欧式距离 当$m=1$时，有 \(D_{m}(\mathbf{X_{i},\mathbf{X_{j}}})= \sum_{k=1}^{n}\vert x_{ik}-x_{jk}\vert\) 此时即为曼哈顿距离

汉明距离

如果模式向量各分量仅取1或(-1)，即为二值模式。 用汉明距离来衡量相似性 \(D_{h}(\mathbf{X_{i}},\mathbf{X_{j}})=\frac{1}{2}\left( n-\sum_{k=1}^{n}x_{ik} \cdot x_{jk} \right)\) 如果各分量取值均不同，则汉明距离为$n$；若各分量取值均相同，则汉明距离为0

角度(余弦)相似度

\[\cos \theta = S(\mathbf{X_{i},X_{j}}) = \frac{\mathbf{X_{i}^T X_{j}}}{\vert \vert \mathbf{X_{i}} \vert\vert \cdot \vert\vert\mathbf{X_{j}}\vert\vert}\]
  • 越接近1代表相似度越大
  • 模式向量$\mathbf{X_{i},X_{j}}$之间的夹角余弦，也是对应的两个单位向量的点积
  • 对坐标系旋转、放大缩小不变
  • 当取值仅为01二值时，$\mathbf{X_{i}^T X_{j}}$的值表示两向量共有的特征数目，而$\vert \vert \mathbf{X_{i}}\vert\vert \cdot \vert\vert\mathbf{X_{j}}\vert\vert = \sqrt{ (\mathbf{X_{i}^T X_{i}})(\mathbf{X_{j}^T X_{j}}) }$表示两向量中具有特征数目的几何平均。于是$S(\mathbf{X_{i},X_{j}})$表示两向量中具有共有特征数目的相似性测度

Tanimoto相似度(考)

Tanimoto测度（通常称为Tanimoto系数或Tanimoto相似度）是用于衡量两个样本（通常是向量或集合）相似性的一种指标。它是Jaccard相似系数的一种推广，尤其常用于二值向量、集合、或化学分子结构的比较。在特定领域，如化学信息学，它被广泛用于比较分子指纹特征的相似性。

定义：

给定两个集合 $A$ 和 $B$，Tanimoto系数的定义与Jaccard相似系数类似，公式为：

\[T(A, B) = \frac{|A \cap B|}{|A \cup B|}\]

其中：

  • $ A \cap B $ 是集合 $A$ 和 $B$ 的交集的大小，表示它们的共同元素的数量。
  • $ A \cup B $ 是集合 $A$ 和 $B$ 的并集的大小，表示它们的所有不同元素的总数。

对于二进制向量（0和1构成的向量），Tanimoto系数可以推广为如下公式：

\[T(\mathbf{x}, \mathbf{y}) = \frac{\mathbf{x} \cdot \mathbf{y}}{|\mathbf{x}|^2 + |\mathbf{y}|^2 - \mathbf{x} \cdot \mathbf{y}}=\frac{共有的特征数}{占有的特征数目的总数}\]

其中：

  • $\mathbf{x} \cdot \mathbf{y}$ 表示两个向量的点积。
  • $ \mathbf{x} ^2$ 和 $ \mathbf{y} ^2$ 是向量 $\mathbf{x}$ 和 $\mathbf{y}$ 的范数（向量长度）的平方。
解释：
  1. 值范围：Tanimoto系数的值在0和1之间：
    • 当两个集合（或向量）完全相同，Tanimoto系数为1。
    • 当两个集合没有任何共同元素，Tanimoto系数为0。
  2. 应用：Tanimoto系数经常用于以下领域：
    • 集合相似性：用于评估两个集合的相似度，尤其是在文档分类或推荐系统中。
    • 化学信息学：用于比较分子指纹，帮助寻找具有相似化学性质的分子。
    • 机器学习和数据挖掘：在特征选择和相似性度量中，尤其是在稀疏向量或二值数据（如推荐系统的用户行为数据）中使用。

聚类准则

根据相似性测度确定的，衡量模式之间是否相似的标准。即把不同模式聚为一类，还是归为不同类的准则(考)

确定方式：

  • 阈值准则：根据规定的距离阈值进行分类
  • 函数准则：根据聚类准则函数进行分类的准则

函数准则

误差平方和 \(J=\sum_{j=1}^{c}\sum_{\mathbf{X}\in S_{j}} \vert\vert\mathbf{X-M_{j}}\vert\vert^2\) 其中，$c$表示共有$c$个模式类，$\mathbf{M_{j}}=\frac{1}{N}\sum_{\mathbf{X}\in S_{j}}\mathbf{X}$，为$S_{j}$中样本的均值向量，$N_{j}$为$\mathbf{S_{j}}$中的样本数目

当$J$达到极小时，说明达到了满意的分类效果。这种准则通常称为最小方差划分 适用于各类样本密集且数量相差不多，而不同类间样本又明显分开的情况

基于距离阈值的聚类算法

近邻聚类法

  1. 任取样本$X_{i}$ 作为第一个聚类中心的初始值，如令$Z_{1}=X_{1}$ 。
  2. 计算样本$X_{2}$ 到$Z_{1}$ 的欧氏距离$D_{21}=\vert\vert X_{2}-Z_{1}\vert\vert$， 若$D_{21}>T$，定义一新的聚类中心$Z_{2} = X_{2}$ ； 否则 $X_{2} ∈$以$Z_{1}$为中心的聚类。
  3. 假设已有聚类中心$Z_{1},Z_{2}$，计算$D_{31}=\vert\vert X_{3}-Z_{1}\vert\vert$和$D_{32}=\vert\vert X_{3}-Z_{2}\vert\vert$ 若$D_{31}>T$且$D_{32}>T$，则建立第三个聚类中心$Z_{3}=X_{3}$ 否则 $X_{3} ∈$离$Z_{1}$和$Z_{2}$最近的聚类。

算法特点

  1. 局限性：很大程度上依赖于第一个聚类中心的位置选择、待分类模式样本的排列次序、距离阈值T的大小以及样本分布的几何性质等。
  2. 优点：计算简单。（一种虽粗糙但快速的方法）

最大最小距离算法(小中取大)

  1. 选任意一模式样本做为第一聚类中心$Z_{1}$
  2. 选择离$Z_{1}$距离最远的样本作为第二聚类中心$Z_{2}$
  3. 逐个计算各模式样本与已确定的所有聚类中心之间的距离，并选出其中的最小距离。例当聚类中心数k=2时，计算$D_{i_{1}}=\vert\vert x_{1}-z_{1}\vert\vert, D_{i_{2}}= \vert\vert x_{1} - z_{2} \vert\vert$，找到$D_{i_{1}}, D_{i_{1}}$最小值 $\min (D_{i_{1}}, D_{i_{2}})$
  4. 在所有最小距离中选出最大距离，如该最大值达到$\vert\vert Z_{1}-Z_{2}\vert\vert$的一定分数比值(阈值$T$) 以上，则相应的样本点取为新的聚类中心，返回3；否则，寻找聚类中心的工作结束。 例如$k=2$，若$\max{\min(D_{i_{1}},D_{i_{2}})}>\theta\vert\vert Z_{1}-Z_{2}\vert\vert$，则$Z_{3}$存在
  5. 重复步骤3,4，直到没有新的聚类中心出现为止。
  6. 将样本${X_{i}, i=1,2,\dots,N}$按最近距离划分到相应聚类中心对应的类别中。 image.png

层次聚类法

每个样本先自成一类，然后按距离准则逐步合并，减少类数。

算法描述

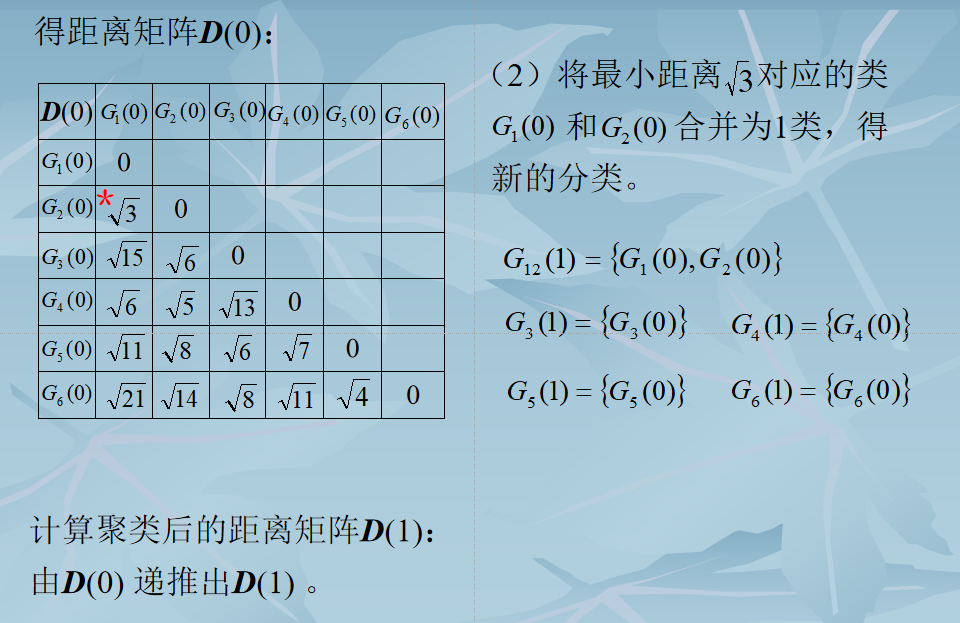
  1. N个初始模式样本自成一类，即建立$N$类： \(G_{1}(0),G_{2}(0),\dots,G_{N}(0)\) 计算各类之间（即各样本间）的距离，得一$N×N$维距离矩阵D(0)。“0”表示初始状态。
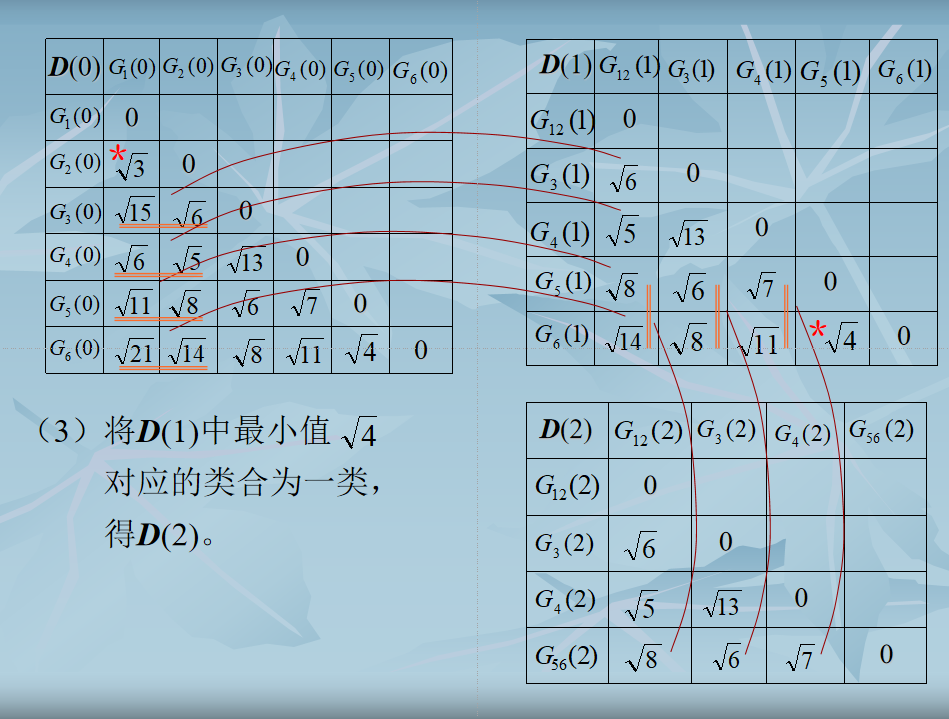
  2. 假设已求得距离矩阵$D(n)$(n为逐次聚类合并的次数)，找出$D(n)$中的最小元素，将其对应的两类合并为一类。由此建立新的分类：$G_{1}(n+1),G_{2}(n+1)$
  3. 计算合并后新类别之间的距离，得$D(n+1)$。
  4. 跳至第2步，重复计算及合并。

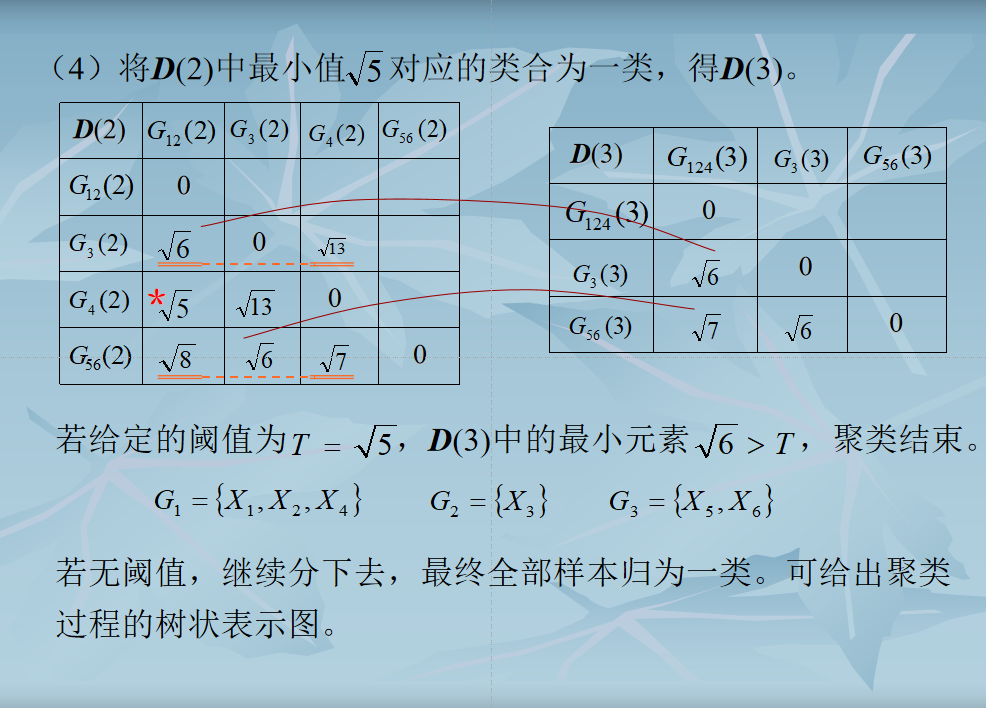
结束条件

  1. 取距离阈值$T$，当$D(n)$的最小分量超过给定值 $T$ 时，算法停止。所得即为聚类结果。
  2. 或不设阈值T，一直将全部样本聚成一类为止，输出聚类的分级树

类间距离计算

最短距离法

\(D_{HK}=\min\{D(X_{H},X_{k})\} X_{H} \in H, X_{K} \in K\) $D(X_{H},X_{K})$ H类中的某个样本$X_{H}$和K类中的某个样本$X_{K}$之间的欧式距离

最长距离法

\[D_{HK}=\max\{D(X_{H},X_{k})\} X_{H} \in H, X_{K} \in K\]

中间距离法

如果K类由I类和J类合并而成，则H和K类之间的距离为

\[D_{HK}=\sqrt{ \frac{1}{2}D_{HI}^2 + \frac{1}{2} D_{HJ}^2 - \frac{1}{4} D_{IJ}^2}\]

重心法

将每类中包含的样本数考虑进去。若$I$类中有$n_{I}$个样本，$J$类中有$n_{J}$个样本，则类与类之间的距离递推式为
\(D_{HK}=\sqrt{ \frac{n_{I}}{n_{I}+n_{J}}D_{HI}^2 + \frac{n_{J}}{n_{I}+n_{J}} D_{HJ}^2 - \frac{n_{I}n_{J}}{(n_{I}+n_{J})^2} D_{IJ}^2}\)

类平均距离

\(D_{HK}=\sqrt{ \frac{1}{n_{H}n_{K}}\sum_{i \in H, j \in K} d_{ij}^2 }\) $d_{ij}^2$: H类任一样本$X_{i}$和K类任一样本$X_{j}$之间的欧氏距离平方。

(考) image.png

image.png

image.png

image.png

Ward’s 簇间距离

\[\begin{equation} \begin{aligned} d(C_{k},C_{j}) &= \sqrt{ 2\times \left( \sum_{x \in C_{k} \cup C_{j}} dist(x, \mu_{C_{k} \cup C_{j}})^2 - \left( \sum_{x \in C_{k}}dist(x, \mu_{C_{k}})^2+ \sum_{x \in C_{j}}dist(x, \mu_{C_{j}})^2\right) \right)} \\ &=\sqrt{ \frac{2 \cdot count(C_{k}) \cdot count(C_{j})}{count(C_{k}) + count(C_{j})} }\cdot dist(\mu_{C_{k}},\mu C_{j}) \\&= \sqrt{ 2\times (SST(C_{k}\cup C_{j})-(SST(C_{k})+SST(C_{j}))) } \end{aligned} \end{equation}\] 
clustering_algorithms = (
    ('Single linkage', 'single'),
    ('Average linkage', 'average'),
    ('Complete linkage', 'complete'),
    ('Ward linkage', 'ward'),
)

for name, method in clustering_algorithms:

    # 绘制树形图
    fig, ax = plt.subplots()
    
    plt.title(name)
    dend = dendrogram(linkage(X, 
                              method = method))
    
    # 层次聚类
    cluster = AgglomerativeClustering(n_clusters=3, 
                                      metric='euclidean', 
                                      linkage=method)
    
    # 完成聚类预测
    Z = cluster.fit_predict(X)
    
    # 可视化聚类结果
    fig, ax = plt.subplots()
    plt.title(name)
    
    # 可视化散点图
    plt.scatter(x=X[:, 0], y=X[:, 1], c=Z, alpha=1.0, 
                    linewidth = 1, edgecolor=[1,1,1])
    
    ax.set_xticks(np.arange(4, 8.5, 0.5))
    ax.set_yticks(np.arange(1.5, 5, 0.5))
    ax.set_xlim(4, 8)
    ax.set_ylim(1.5, 4.5)
    plt.xlabel(iris.feature_names[0])
    plt.ylabel(iris.feature_names[1])
    ax.grid(linestyle='--', linewidth=0.25, color=[0.5,0.5,0.5])
    ax.set_aspect('equal')
    plt.show()

基于密度的聚类

[!note] 本部分主要介绍DBSCAN，其余方法作为补充

基本概念

DBSCAN算法包含以下几个基本概念：

  • $\varepsilon$邻域：对于一个给定的数据点，$\varepsilon$邻域是指在其半径$\varepsilon$范围内的所有数据点的集合。$\varepsilon$是一个用户定义的距离参数。
  • MinPts阈值(min_samples)：MinPts是定义一个点是否为核心点的阈值。一个点的$\varepsilon$邻域内至少包含MinPts个数据点，该点才被认为是核心点。
  • 核心点：如果一个点的$\varepsilon$邻域内包含至少MinPts个点，则该点是一个核心点。
  • 边界点：边界点是指在核心点的$\varepsilon$邻域内，但自身的$\varepsilon$邻域内的点数小于MinPts的点。
  • 噪声点：既不是核心点也不是边界点的点被称为噪声点。
  • 密度可达：如果点P在点Q的$\varepsilon$邻域内，并且Q是核心点，那么点P是从点Q密度可达的。
  • 密度连接：如果存在一个点链，使得每一对相邻点之间都是密度可达的，那么两个点之间就是密度连接的。

聚类过程

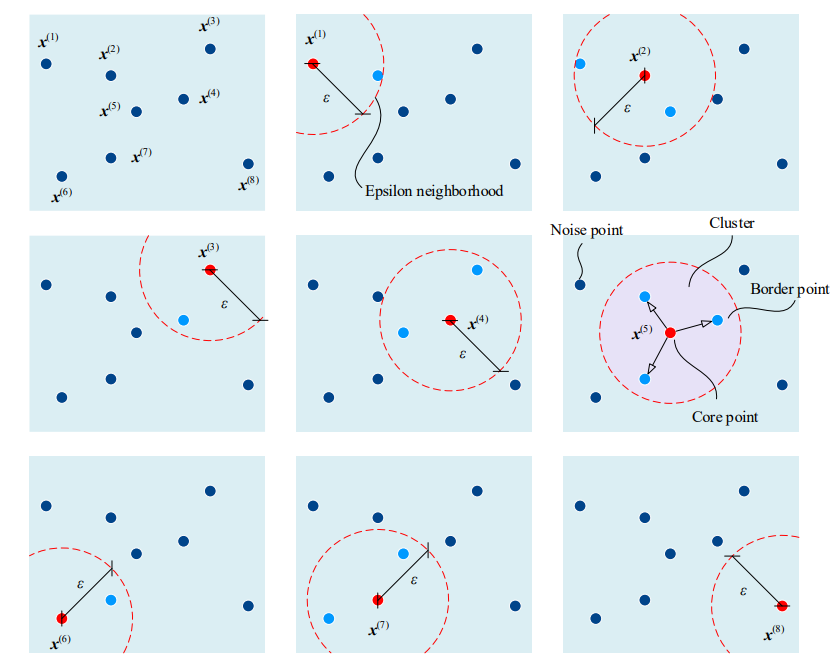
给出平面内8个样本数据点，以每个数据点为中心，$ε$ 为半径扫描整个平面，且定义 min_samples = 4。 发现只有样本点 $x (5)$的 $ε$ 邻域内有 4 个样本点 (包括 $x (5)$自身)；因此，$x5$为核心点，$x (2)、x (4)和 x (7)$为 边界点，剩余其他数据点为噪点。 image.png

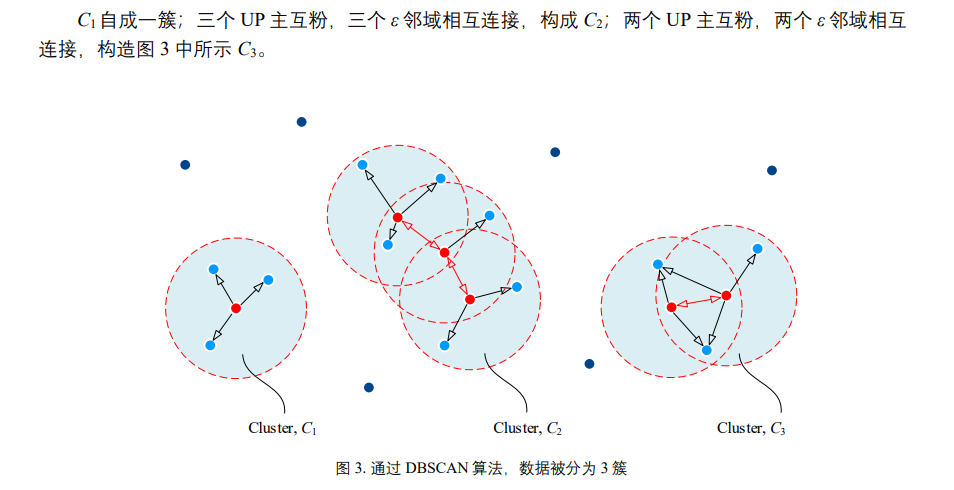
如果一个点既是边界点又是核心点，那么此时会有两个簇连接在一起，以此类推： image.png

调节参数

邻域范围

eps 控制邻域范围大小。eps 值选取过大，会导致整个数据集被分为一簇；但是 eps 取值过小，会 导致簇过多且分散，并且标记过多噪音点。

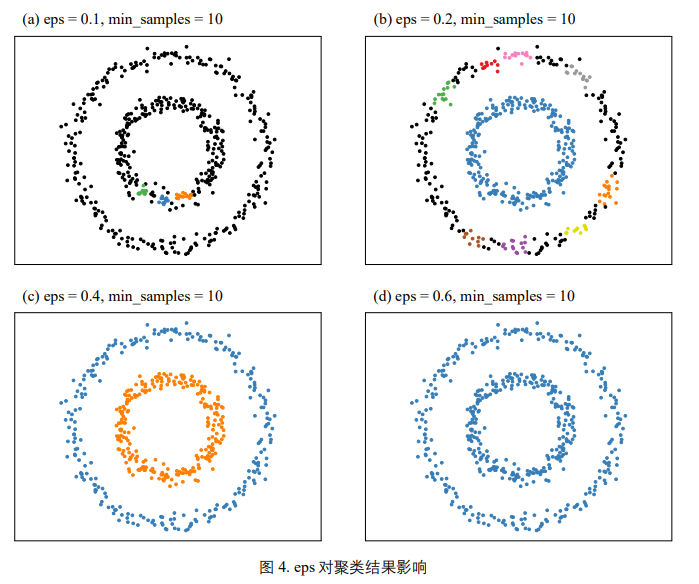
image.png

for eps in np.array([0.1,0.2,0.4,0.6]):
    
    dbscan = cluster.DBSCAN(eps=eps,min_samples=10)

    y_pred = dbscan.fit_predict(X)

    fig, ax = plt.subplots()

    colors = np.array(list(islice(cycle(['#377eb8', '#ff7f00', '#4daf4a',
                                         '#f781bf', '#a65628', '#984ea3',
                                         '#999999', '#e41a1c', '#dede00']),
                                  int(max(y_pred) + 1))))
    # 增加黑色
    colors = np.append(colors, ["#000000"])
    # 绘制散点图
    plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])
    
    plt.title('eps = %0.2f' % eps)
    plt.xlim(-2.5, 2.5)
    plt.ylim(-2.5, 2.5)
    plt.xticks(())
    plt.yticks(())
    plt.axis('equal')

plt.show()

邻域内样本个数

min_samples 调节 DBSCAN 算法对噪声的容忍度；当数据噪音过大时，应该适当提高 min_samples。 k 均值和 GMM 聚类算法需要预先声明聚类数量；但是，DBSCAN 则不需要。DBSCAN 聚类不需要 预设分布类型，不受数据分布影响，且可以分辨离群数据。 DBSCAN 算法对 eps 和 min_samples 这两个初始参数都很敏感；协同调节 eps 和 min_samples 两个参数显得非常重要。

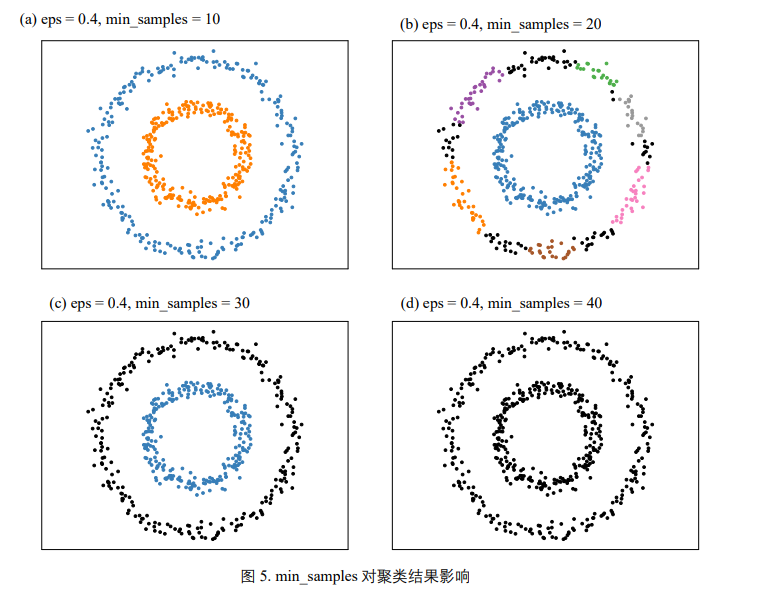
image.png

优点：

  • 无需指定簇的个数：与K-means等算法不同，DBSCAN不需要预先指定聚类的数量。
  • 处理噪声：能够有效识别并处理噪声点。
  • 发现任意形状的簇：能够发现任意形状的簇，而不仅仅是圆形或球形的簇。

缺点：

  • 参数敏感：算法对参数Eps和MinPts较为敏感，选择不当会影响聚类结果。
  • 性能问题：在高维数据集上性能不佳，计算Eps邻域的时间复杂度为O(n^2)，对于大规模数据集不够高效。
  • 不适用于不同密度的簇：如果数据集中的簇有显著不同的密度，DBSCAN可能无法很好地识别所有簇。
  • 对密度分布较为均匀的数据集，可能会出现聚类失效

动态聚类

K-means(考计算)

比如，二聚类问题有两个簇质心$\mu_{1}$和$\mu_{2}$ 如果以欧式距离进行距离度量，那么离质心$\mu_{1}$更近的点，被划分为$C_{1}$簇；反之被划分为$C_{2}$簇

由于采用欧氏距离，图 1中簇质心 $µ_{1}$ 和 $µ_{2}$等高线为两组同心圆；同心圆颜色相同，代表距离簇质心 $µ_{1}$ 和 $µ_{2}$距离相同。因此，同色同心圆的交点位于决策边界上。

实际上就是质心之间的中垂线 三聚类时更加明显：

优化目标

将所有样本点划分为$K$簇，并使得簇内距离平方和最小 \(\arg \min_{c} \sum_{k=1}^{K} \sum_{x \in C_{k}} ||x - \mu_{k}||^2\)

对于每一个聚类集，将准则函数定义为 \(J_{j} = \sum_{x \in C_{j}} ||x - \mu_{j}||^2\) 由于要使得准则函数最小，对其求偏导 \(\frac{\partial}{\partial \mu_{j}} \sum_{x \in C_{j}} ||x - \mu_{j}||^2 = \frac{\partial}{\partial \mu_{j}} \sum_{x \in C_{j}}(x-\mu_{j})^T(x-\mu_{j})=0\) 需要对其进行展开 \(\frac{\partial}{\partial \mu_{j}} \sum_{x \in C_{j}}(x-\mu_{j})^T(x-\mu_{j})=\frac{\partial}{\partial \mu_{j}} \sum_{x \in C_{j}}(x^Tx-2x^T\mu_{j}+\mu_{j}^2)=\sum_{x \in C_{j}}(-2x^T+2\mu_{j})=0\) 其中，$-2$可以消去，再次进行展开 \(\sum_{x \in C_{j}} x^T = \sum_{x \in C_{j}} \mu_{j}\) 由于$\mu_{j}$与$x$无关，故可提到求和之外，右侧可化简 \(\sum_{x \in C_{j}} x^T = |C_{j}| \mu_{j}\) 解得 \(\mu_{j} = \frac{1}{|C_{j}|}\sum_{x \in C_{j}} x^T\) 说明$C_{j}$类的聚类中心应为该类样本的均值

迭代过程

此处$Z_i$和$\mu_{i}$意思等同，只是因为老师强制要求符号这么写，所以进行记录

  1. 任选K个初始聚类中心：$Z_{1}(1)$， $Z_{2}(1)$，…， $Z_{K}(1)$。(括号内序号表示迭代运算的次序号)
  2. 按最小距离原则将其余样品分配到K个聚类中心中的某一个，即：
\[若\min \{||x-Z_{i}(k)||\}=||x-Z_{j}(k)|| = D_{j}(k), 则X \in C_{j}(k)\]
  1. 计算各个聚类中心的新向量值：$Z_{j}(k+1),j=1,2,\dots,K$
\[Z_{j}(k+1)=\frac{1}{|C_{j}|}\sum_{x \in C_{j}(k)}{x},\ j = 1,2,\dots,K\]
  1. 如果$Z_{j}(k+1) \neq Z_{j}(k), j=1,2,\dots,K$，回到(2)，重新分类迭代计算；如果取等，此时算法收敛

image.png image.png image.png image.png image.png

代码1 (比较复杂可以不看)

# 导入鸢尾花数据
iris = datasets.load_iris()
# 取出鸢尾花前两个特征
X_train = iris.data[:, :2]
y_train = iris.target

# 创建KMeans对象
kmeans = KMeans(n_clusters=3, n_init = 'auto')
# 使用KMeans算法训练数据
kmeans.fit(X_train)

# 生成网格数据
plot_step = 0.02
xx, yy = np.meshgrid(np.linspace(4, 8, int(4/plot_step + 1)),
                     np.linspace(1.5, 4.5, int(3/plot_step + 1)))

# 使用KMeans模型对网格中的点进行预测
# 并将预测结果整形成与网格相同形状的矩阵
Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

fig, ax = plt.subplots()

# plot regions
plt.contourf(xx, yy, Z, cmap=cmap_light)

# plot sample data
plt.scatter(x=X_train[:, 0], y=X_train[:, 1], color=np.array([0, 68, 138])/255., alpha=1.0, linewidth = 1, edgecolor=[1,1,1])

# plot decision boundaries
plt.contour(xx, yy, Z, levels=[0,1,2], colors=np.array([0, 68, 138])/255.)

# plot centroids
centroids = kmeans.cluster_centers_

plt.scatter(centroids[:, 0], centroids[:, 1], marker="x", s=100, linewidths=1.5, color="k")

ax.set_xticks(np.arange(4, 8.5, 0.5))
ax.set_yticks(np.arange(1.5, 5, 0.5))
ax.set_xlim(4, 8)
ax.set_ylim(1.5, 4.5)
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
ax.grid(linestyle='--', linewidth=0.25, color=[0.5,0.5,0.5])
ax.set_aspect('equal')
plt.show()
1. np.meshgrid() 和生成网格数据

np.meshgrid 是用来生成二维坐标网格的函数，它会根据提供的输入向量生成两个矩阵，表示网格点的横坐标和纵坐标。

解释代码：

plot_step = 0.02
xx, yy = np.meshgrid(np.linspace(4, 8, int(4/plot_step + 1)),
                     np.linspace(1.5, 4.5, int(3/plot_step + 1)))
  • plot_step = 0.02：表示网格的间距，每个网格点之间相差 0.02。
  • np.linspace(4, 8, int(4/plot_step + 1))：这部分生成从 4 到 8 之间的等间隔点，步长为 plot_step。生成的点的个数是 int(4/plot_step + 1)，即从 4 到 8 之间一共生成 (8 - 4) / 0.02 + 1 = 201 个点。这个向量表示网格在 x 轴上的坐标。
  • np.linspace(1.5, 4.5, int(3/plot_step + 1))：同理，生成从 1.5 到 4.5 之间的等间隔点，表示 y 轴上的坐标。
  • np.meshgrid()：它会将两个向量（x 和 y 坐标）组合成一个二维网格，这样可以方便地进行二维平面上的计算。xx 表示网格中每个点的 x 坐标，yy 表示网格中每个点的 y 坐标。

例如，xx 和 yy 的形状将会是相同的，它们都是 $201 \times 151$ 的矩阵。xx 的每一行都表示 x 坐标的值，而 yy 的每一列都表示 y 坐标的值。

2. np.c_[xx.ravel(), yy.ravel()]

np.c_ 是 NumPy 用于水平拼接数组的功能，它将多个数组按列进行拼接。

解释代码：

Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])
  • xx.ravel()：将矩阵 xx 拉平成一维数组，按照行优先顺序展平。
  • yy.ravel()：同样，将 yy 展平成一维数组。 xx.ravel() 和 yy.ravel() 现在是两个一维数组，它们的长度均为 (201 \times 151 = 30351)。
  • np.c_[xx.ravel(), yy.ravel()]：将 xx.ravel() 和 yy.ravel() 按列拼接在一起，形成一个形状为 (30351 \times 2) 的二维数组。每一行代表网格中的一个点，第一列是 x 坐标，第二列是 y 坐标。 通过 np.c_[xx.ravel(), yy.ravel()]，我们创建了一个包含所有网格点坐标的二维数组，便于后续使用 KMeans 模型进行预测。
总结：
  • np.meshgrid() 生成了二维平面的网格坐标。
  • np.c_[xx.ravel(), yy.ravel()] 将网格中的每一个点的 x 和 y 坐标组合成一个 $30351 \times 2$ 的数组，表示网格中所有点的坐标，供 kmeans.predict 进行分类。 image.png

代码2 常用

# pandas导入
df = pd.read_csv('./ch1ex1.csv')
points = df.values

xs = points[:, 0]
ys = points[:, 1]

model = KMeans(n_clusters = 3, n_init = 'auto')
model.fit(points)
labels = model.predict(points)
print(labels) # 打印每个点被分到的类

# 聚类中心
centroids = model.cluster_centers_
centroids_x = centroids[:, 0]
centroids_y = centroids[:, 1]

# 原始数据点
xs = points[:, 0]
ys = points[:, 1]

# 建立装饰和颜色
mk0 = ['o', ',', 'v']
cs0 = ['r', 'g', 'b']
mk1 = []
cs1 = []

for e in labels:
    mk1.append(mk0[e])
    cs1.append(cs0[e])

# 画点和质心
plt.figure(figsize=(10, 6), dpi = 120)
plt.subplot(111)
for x, y, cr, m ,in zip(xs, ys, cs1, mk1):
    plt.scatter(x, y, edgecolors=cr, facecolors = 'none', marker=m)
plt.scatter(centroids_x, centroids_y, marker = 'X', s = 200, c = 'k')
plt.show()

肘部系数

用于判断合适的聚类簇值K \(SSE(X|K)=\sum_{k=1}^{K}SSE(C_{k})=\sum_{k=1}^{K}\sum_{x \in C_{k}}||x-\mu_{k}||^2\) 曲线的拐点对应着接近最优的K值（SSE减小量、计算量以及分类效果的权衡）。

seeds_df = pd.read_csv('./seeds-less-rows.csv')
# print(seeds_df.grain_variety.value_counts())
varieties = list(seeds_df['grain_variety'])

samples = seeds_df.values
#print(len(samples))
ks = range(1, 6)
inertias = []

for k in ks:
    #Create a KMeans instance with k clusters: model
    model = KMeans(n_clusters=k, n_init = 'auto')
    #Fit model to samples
    model.fit(samples)
    # Append the inertia to the list of inertias
    inertias.append(model.inertia_)

plt.figure(figsize=(10, 6), dpi=80)
plt.subplot(111)
#plot ks vs inertias
plt.plot(ks, inertias, '-o')
plt.xlabel('number of clusters, k')
plt.ylabel('inertia')
plt.xticks(ks)
plt.show()

image.png

轮廓图：选定聚类簇值

轮廓图上每一条线代表的是轮廓系数： \(s_{i}=\frac{b_{i}-a_{i}}{\max \{a_{i},b_{i}\}}\) 其中，$a_{i}$为簇内不相似度，$b_{i}$为簇间不相似度

簇内不相似度

样本$i \in C_{k}$到同簇其他样本$j(j \in C_{k}, i \neq j)$距离的平均值： \(a_{i}=\frac{1}{count(C_{k})-1}\sum_{j \in C_{k},i\neq j} {d_{i,j}}\) $d_{i,j}$为样本$i$和$j$之间的距离，$a_{i}$越小1，说明越应该被划分到$C_{k}$簇

簇间不相似度

样本$i \in C_{k}$到其他簇样本$j(j \in C_{m}, C_{m} \neq C_{k})$距离的平均值： \(b_{i} = \min \frac{1}{count(C_{m})}\sum_{j \in C_{m}}{d_{i,j}}\)

[!note] 当簇数超过2时，$b_{i}$需要在不同簇中找到最小值

计算轮廓系数的函数为 sklearn.metrics.silhouette_score yellowbrick.cluster.SilhouetteVisualizer 函数绘制轮廓图

from sklearn.cluster import KMeans
from yellowbrick.cluster import SilhouetteVisualizer
from sklearn.metrics import silhouette_score

kmeans = KMeans(n_clusters=n_clusters, random_state=10)
cluster_labels = kmeans.fit_predict(X)

silhouette_avg = silhouette_score(X, cluster_labels)
print("For n_clusters =", n_clusters, "The average silhouette_score is :", silhouette_avg)
# For n_clusters = 3 The average silhouette_score is : 0.445052569

visualizer = SilhouetteVisualizer(kmeans, colors='yellowbrick')

visualizer.fit(X)
# Fit the data to the visualizer
visualizer.show()

沃罗诺伊图

质心中垂线相交分割区域

image.png

迭代自组织(ISODATA)

聚类算法：ISODATA算法 - 华东博客 - 博客园

与K-均值算法的比较

  • K-均值算法通常适合于分类数目已知的聚类，而ISODATA算法则更加灵活；
  • 从算法角度看， ISODATA算法与K-均值算法相似，聚类中心都是通过样本均值的迭代运算来决定的；
  • ISODATA算法加入了一些试探步骤，并且可以结合成人机交互的结构，使其能利用中间结果所取得的经验更好地进行分类。
  • K-均值算法的聚类中心个数不变；ISODATA的聚类中心个数变化。

image.png

算法步骤

第一步：输入$N$个模式样本${x_{i},i=1,2,…,N}$

预选$N_{c}$个初始聚类中心${z_{1},z_{2},…z_{N_{c}}}$，它可以不等于所要求的聚类中心的数目，其初始位置可以从样本中任意选取。

预选： $K$  = 预期的聚类中心数目； $θ_{N}$ = 每一聚类域中最少的样本数目，若少于此数即不作为一个独立的聚类； $θ_{S}$ = 一个聚类域中样本距离分布的标准差；标准差向量的每一分量反映样本在特征空间的相应维上，与聚类中心的位置偏差（分散程度）。要求每一聚类内，其所有分量中的最大分量应小于$θ_{S}$，否则该类将被分裂为两类。 $θ_{c}$ = 两个聚类中心间的最小距离，若小于此数，两个聚类需进行合并； $L$ = 在一次迭代运算中可以合并的聚类中心的最多对数； $I$  = 迭代运算的次数。

第二步：将$N$个模式样本分给最近的聚类$S_{j}$，假若$D_{j}=   x-z_{j}   =min{‖x−z_{i}‖,i=1,2,⋯N_{c}}$，即$   x−z_{j}   $的距离最小，则$x∈S_{j}$。

第三步：如果$S_{j}$中的样本数目$S_{j}<θ_{N}$，则取消该样本子集，此时$N_{c}$减去1。 （以上各步对应基本步骤（1））

第四步：修正各聚类中心 \(z_{j}=\frac{1}{N_{j}}∑_{x∈S_{j}}x,\ j=1,2,⋯,N_{c}\)

第五步：计算各聚类域$S_{j}$中模式样本与各聚类中心间的平均距离 \(\bar{D_{j}}=\frac{1}{N_{j}}∑_{x∈S_{j}}∥x−z_{j}∥,j=1,2,⋯,N_{c}\)

第六步：计算全部模式样本和其对应聚类中心的总平均距离 \(\bar{D}=\frac{1}{N}\sum_{j=1}^{N_{c}}N_{j}\bar{D_{j}}\) （以上各步对应基本步骤（2））

第七步：判别分裂、合并及迭代运算

  1. 若迭代运算次数已达到$I$次，即最后一次迭代，则置$θ_{c} =0$，转至第十一步。
  2. 若$N_{c} ≤ \frac{K}{2}$，即聚类中心的数目小于或等于规定值的一半，则转至第八步，对已有聚类进行分裂处理。
  3. 若迭代运算的次数是偶数次，或$N_c≥2K$，即聚类中心数目大于或等于希望数的两倍，不进行分裂处理，转至第十一步(合并)；否则（即既不是偶数次迭代，又不满足$N_{c}≥2K$），转至第八步，进行分裂处理。 （以上对应基本步骤（3）） image.png

第八步：计算每个聚类中样本距离的标准差向量$σ_{j}=[σ_{j_{1}},σ_{j_{2}},…,σ_{jn}]T$ 其中向量的各个分量为\(\sigma_{ji}=\sqrt{ \frac{1}{N_{j}}\sum_{x \in S_{j}}(x_{ji}-z_{ji})^2 }=\sqrt{ 方差 }\) 式中，$i = 1, 2, …, n$为样本特征向量的维数，$j = 1, 2, …, N_{c}$为聚类数，$N_{j}$为$S_j$中的样本个数。

第九步：求每一标准差向量${σ_{j}, j = 1, 2, …, N_{c}}$中的最大分量，以${σ_{jmax}, j = 1, 2, …, Nc}$代表。

第十步：在任一最大分量集${σ_{jmax}, j = 1, 2, …, N_{c}}$中，若有$σ_{jmax}>θ_{S}$(标准差阈值)，说明$S_{j}$类样本在对应方向上的标准差大于允许的值，同时又满足如下两个条件之一：

  1. $\bar{D_{j}}>\bar{D}$和$N_{j} > 2(θ_{N} + 1)$，即类内平均距离大于总体平均距离，且$S_{j}$中样本总数超过规定值一倍以上($\theta_{N}$为每个聚类中的最少样本数)；
  2. $N_{c} ≤ \frac{K}{2}$，即聚类数小于或等于希望数目的一半。

则将 $z_{j}$ 分裂为两个新的聚类中心$Z_{j}^+$和$Z_{j}^-$，且$N_{c}$加1。$Z_{j}^+ = σ_{jmax}$+$kσ_{jmax}$，$Z_{j}^-=σ_{jmax}-kσ_{jmax}$，$0<k\leq{1}$，称为分裂系数。

如果本步骤完成了分裂运算，迭代次数+1，则转至第二步，否则继续。 （以上对应基本步骤（4）进行分裂处理）

合并处理： 第十一步：计算全部聚类中心的距离 \(D_{ij}=||z_{i}−z_{j}||，i=1,2,…,N_{c}−1，j=i+1,…,N_{c}\)

第十二步：比较$D_{ij}$与$θ_{c}$(两聚类中心的最小距离)的值，将$D_{ij} <θ_c$ 的值按最小距离次序递增排列，即 \(\{D_j_{1}},D_{i_{2}j_{2}},…,D_{i_{L}j_{L}}\}\) 式中$D_j_{1}}<D_{i_{2}j_{2}}<…<D_{i_{L}j_{L}}$。

第十三步：将距离为$D_{i_{k}j_{k}}$的两个聚类中心$Z_{ik}$和$Z_{jk}$合并，得新的中心为： \(z^∗_{k}= \frac{1}{N_{ik}+N_{jk}} [N_{ik}z_{ik}+N_{jk}z_{jk}],k=1,2,⋯,L\) 式中，被合并的两个聚类中心向量分别以其聚类域内的样本数加权，使$Z^∗_{k}$为真正的平均向量。 （以上对应基本步骤（5）进行合并处理）

第十四步：如果是最后一次迭代运算（即第$I$次），则算法结束；否则，若需要操作者改变输入参数，转至第一步；若输入参数不变，转至第二步。 在本步运算中，迭代运算的次数每次应加1。